CRC32算法
CRC校验实用程序库在数据存储和数据通讯领域,为了保证数据的正确,就不得不采用检错的手段。在诸多检错手段中,CRC是最著名的一种。CRC的全称是循环冗余校验,其特点是:检错能力极强,开销小,易于用编码器及检测电路实现。从其检错能力来看,它所不能发现的错误的几率仅为0.0047%以下。从性能上和开销上考虑,均远远优于奇偶校验及算术和校验等方式。
因而在数据存储和数据通讯领域,CRC无处不在:著名的通讯协议X.25的FCS(帧检错序列)采用的是CRC-CCITT,ARJ、LHA等压缩工具软件采用的是CRC32,磁盘驱动器的读写采用了CRC16,通用的图像存储格式GIF、TIFF等也都用CRC作为检错手段。简而言之,CRC是一个数值。该数值被用于校验数据的正确性。CRC数值简单地说就是通过让你需要做处理的数据除以一个常数而得到的余数。当你得到这个数值后你可以将这个数值附加到你的数据后,当数据被传送到其他地方后,取出原始数据(可能在传送过程中被破坏)与附加的CRC数值,然后将这里的原始数据除以之前那个常数(约定好的)然后得到新的CRC值。比较两个CRC值是否相等即可确认你的数据是否在传送过程中出现错误。
那么如何让数据除以一个常数?方法是对你的数据进行必要的编码处理,逐字节处理成数字。那么这个常数是什么?你不必关注它是什么,也不需要关注它是如何获得的。当你真的要动手写一个CRC的实现算法时,我可以告诉你,CRC的理论学家会告诉你。不同长度的常数对应着不同的CRC实现算法。当这个常数为32位时,也就是这里所说的CRC32。
CRC的本质是模-2除法的余数,采用的除数不同,CRC的类型也就不一样。通常,CRC的除数用生成多项式来表示。由于CRC在通讯和数据处理软件中经常采用,笔者在实际工作中对其算法进行了研究和比较,总结并编写了一个具有最高效率的CRC通用程序库。该程序采用查表法计算CRC,在速度上优于一般的直接模仿硬件的算法,可以应用于通讯和数据压缩程序。因此很多教科书会把CRC与多项式关联起来。这里的多项式指的是系数为0或1的式子,例如:a0 + a1*x + a2*x^2 + ... + an*x^n。其中a0, a1, ..., an要么为0要么为1。我们并不关注x取什么值。(如果你要关注,你可以简单地认为x为2) 这里把a0, a1, ..., an的值取出来排列起来,就可以表示比特流。例如 1 + x + x^3所表示的比特流就为:1101。部分资料会将这个顺序颠倒,这个很正常。
通常的CRC算法在计算一个数据段的CRC值时,其CRC值是由求解每个数值的CRC值的和对CRC寄存器的值反复更新而得到的。这样求解CRC的速度较慢。通过对CRC算法的研究,我们发现:一个8位数据加到16位累加器中去,只有累加器的高8位或低8位与数据相作用,其结果仅有256种可能的组合值。因而我们可以用查表法来代替反复的运算,这也同样适用于CRC32的计算。
CRC算法通过计算一个固定长度的校验码,将该校验码附加到原始数据的末尾,接收方在接收到数据后重新计算校验码并与接收到的校验码进行比较,以此判断数据在传输过程中是否发生了错误。这种校验机制不仅能够检测出大多数类型的错误,而且计算效率高,占用资源少,因此在各种通信协议、文件系统、磁盘驱动器和网络协议中都有广泛应用。其原理基于多项式除法。在CRC校验中,数据被视为一个系数为0或1的多项式序列,而CRC校验码则是通过使用一个预定义的生成多项式对该数据多项式进行模2除法运算得到的。生成多项式的选择对CRC算法的错误检测能力有重要影响,通常选取的生成多项式能够检测出尽可能多类型的错误。在计算CRC校验码时,原始数据与生成多项式的模2除法的结果被附加到数据的末尾,形成一个完整的数据包。在接收端,同样使用生成多项式对数据包进行模2除法,如果余数为零,则认为数据在传输过程中未发生错误。
具体实现过程如下:
1.将待发送的数据视为一个二进制多项式D(x),其中每一位代表一个系数。
2.选取一个生成多项式G(x),该多项式的长度决定了CRC校验码的长度。
3.对D(x)乘以x^n(n为生成多项式的长度减1),形成一个与G(x)同阶的多项式。
4.使用生成多项式G(x)对该扩展后的多项式进行模2除法,得到的余数即为CRC校验码。
5.将CRC校验码附加到原始数据的末尾,形成完整的数据包。
6.在接收端,对数据包再次进行相同的模2除法运算,若余数为零,则认为数据包未发生错误。
CRC校验算法在实际应用中非常灵活,可以通过选择不同的生成多项式来适应不同场合的需求。例如,CRC-32使用一个32位的生成多项式,可以检测出绝大多数常见的错误类型,包括所有奇数位错误、所有双位错误(在数据长度不超过31位的情况下)、所有突发错误(长度小于等于32位)以及大多数长度超过32位的突发错误。
在C语言中实现CRC算法时,可以利用位运算和循环结构来高效地完成模2除法运算。下面是使用标准C库函数和位运算符来实现CRC-32算法示例:
#include <stdint.h>
uint32_t crc32(const unsigned char *buf, size_t len) {
uint32_t crc = 0xFFFFFFFF;
const unsigned char *end = buf + len;
uint32_t table[256];
// Pre-compute the CRC table
for (int i = 0; i < 256; i++) {
uint32_t c = i;
for (int j = 0; j < 8; j++) {
if (c & 1) {
c = 0xEDB88320 ^ (c >> 1);
} else {
c = c >> 1;
}
}
table[i] = c;
}
// Process each byte of the data
while (buf < end) {
crc = table[(crc ^ *buf++) & 0xFF] ^ (crc >> 8);
}
return crc ^ 0xFFFFFFFF;
}
这段代码首先预计算了一个CRC表,用于加速后续的模2除法运算,然后逐字节处理输入数据,最终返回CRC校验码。通过这种方式,CRC算法能在保证准确性的同时,达到较高的计算速度,满足实时性和效率的要求。CRC校验算法凭借其高效的错误检测能力,在数据通信和存储系统中发挥着不可或缺的作用。无论是嵌入式系统、网络通信还是文件系统,CRC都是确保数据完整性和可靠性的一种重要手段。
什么是生成多项式?
所谓的生成多项式,就是上面我所说的常数。注意,在这里,一个多项式就表示了一个比特流,也就是一堆1、0,组合起来最终就是一个数值。例如CRC32算法中,这个生成多项式为:c(x) = 1 + x + x^2 + x^4 + x^5 + x^7 + x^8 + x^10 + x^11 + x^12 + x^16 + x^22 + x^23 + x^26 + x^32。
其对应的数字就为:11101101101110001000001100100000(x^32在实际计算时隐含给出,因此这里没有包含它的系数),也就是0xEDB88320(多项式对应的数字可能颠倒,颠倒后得到的是0x04C11DB7,其实也是正确的)。 由此可以看出,CRC值也可以看成我们的数据除以一个生成多项式而得到的余数。
如何做这个除法?
套用大部分教科书给出的计算方法,因为任何数据都可以被处理成纯数字,因此,在某种程度上说,我们可以直接开始这个除法。尽管事实上这并不是标准的除法。例如,我们的数据为1101011011(方便起见我直接给二进制表示了,从这里也可以看出,CRC是按bit进行计算的),给定的生成多项式(对应的值)为10011。通常的教科书会告诉我们在进行这个除法前,会把我们的数据左移几位(生成多项式位数-1位),从而可以容纳将来计算得到的CRC值(我上面所说的将CRC值附加到原始数据后)。但是为什么要这样做?我也不知道(不知道的东西不能含糊而过)。那么,除法就为:
1100001010
_______________
10011 ) 11010110110000 附加了几个零的新数据
10011......... 这里的减法(希望你不至于忘掉小学算术)是一个异或操作
-----.........
10011........
10011........
-----........
00001....... 逐bit计算
00000.......
-----.......
00010......
00000......
-----......
00101.....
00000.....
-----.....
01011....
00000....
-----....
10110...
10011...
-----...
01010..
00000..
-----..
10100.
10011.
-----.
01110
00000
-----
1110 = 这个余数也就是所谓的CRC值,通常又被称为校验值。
希望进行到这里,你可以获取更多关于CRC的感性认识。而我们所要做的,也就是实现一个CRC的计算算法。说白了,就是提供一个程序,给定一段数据,以及一个生成多项式(对于CRC32算法而言该值固定),然后计算得出上面的1110余数。
CRC32算法冲突概率
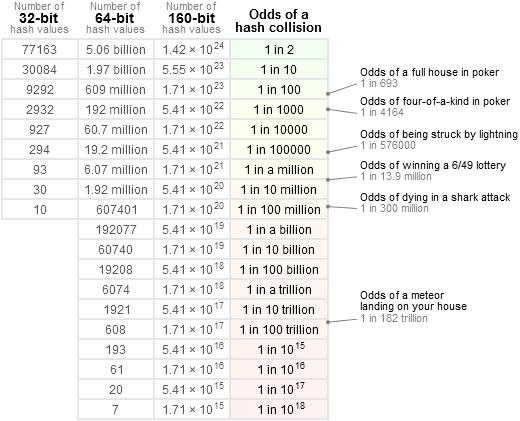
1)、CRC32在完全随机的输入情况下,冲突概率还是比较高的,特别是到了1亿的数据量后,冲突概率会更高。
2)、CRC32在输入某个连续段的数据情况下,冲突概率反而很低,这是因为两个冲突的原值理论上应该是相隔很远,只输入某段数据的情况下,这个段里面冲突的原值会很少。
上文对CRC进行了简略的介绍,接下来对其进行较为详细的讲解,并提供一些代码实现。CRC 也叫循环冗余校验码,它属于密码学一类算法,常用于数据校验,一般会用来检测程序是否被脱壳或者被修改,以达到防破解的目的。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。CRC 运算实际上就是将数据 k 进行模 2 运算,得到余数 n,然后将 n 拼接到 k 的后面生成 k+n 为循环冗余校验码的字长。接着发送 k+n 到接收方作为被除数进行模 2 运算,判断余数是否为 0,如果余数非 0 则 CRC 检测出数据被修改了。简单点说就是把需要校验的数据与生成多项式进行循环异或处理:
1.发送方和接受方会约定一个特定的除数,它是一个定值,我们也叫除数为生成多项式;
2.在计算余数时,被除数也就是数据 k 需要进行补 0,补 0 个数为生成多项式长度 - 1 个 0;
3.余数长度一定与补零的长度一致。
流程图:
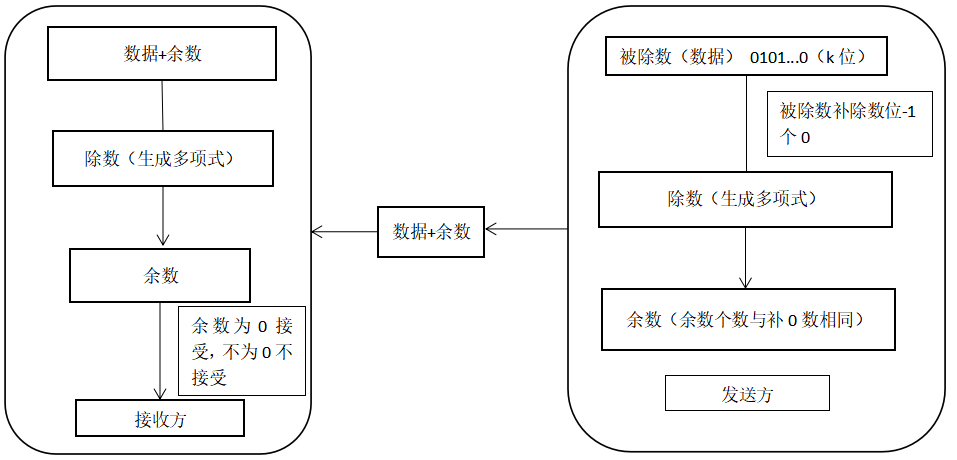
示例如下
例1:这里数据为 1110101,生成多项式为 101,那么我们要传给接收方的数据就为 1110101(数据)+10(余数)=111010110

这个就是 CRC 的计算原理了,其算法参数模型解释:
NAME:参数模型名称。
WIDTH:宽度,即CRC比特数。
POLY:生成项的简写,以16进制表示。例如:CRC-32即是0x04C11DB7,忽略了最高位的"1",即完整的生成项是0x104C11DB7。
INIT:这是算法开始时寄存器(crc)的初始化预置值,十六进制表示。
REFIN:待测数据的每个字节是否按位反转,True或False。
REFOUT:在计算后之后,异或输出之前,整个数据是否按位反转,True或False。
XOROUT:计算结果与此参数异或后得到最终的CRC值。
CRC 计算的两种方式
1. 直接计算法
这里通过例子来讲解,例2:

首先看到这里的生成项是 1101,然后在计算中的除数(蓝色字体标记)大多是 1101 而有时是 0000,当除数为 1101 时被除数的首位都是 1,而首位不为 1 时就是 0000。那么不妨做个假设,既然被除数和除数的首位为 1 时会被消掉那么我们就不需要四位异或了,改成三位异或,三位异或的话被除数一次就取三个,而除数取后三个,当被除数首位为 1 时就左移一位让新的三位与除数(生成项)的后三位进行异或;当被除数移出位是 0 时就异或 000,然后不断重复此步骤直至结束。(这里是针对本例题的,当你的生成项为 n 时,你就取 n-1 位异或)
那么就会有人问到底需要重复几次才算结束呢?
处理次数 = 待处理数据位数(被除数位数)= 商的位数(本题次数为 6 次)
例如本题第一次被除数取 100,左移一位得 001 然后与 101 异或得 100。100 左移一位得 000 然后与 101 异或得 101。101 左移一位得 010 然后与 101 异或得 111。111 左移一位得 110 然后与 101 异或得 011。011 左移一位得 110 然后与 000 异或得 110(与 000 异或值是不变的)。110 左移一位得 100 然后与 101 异或得 001 得到余数刚好 6 次。
2. 驱动表法
驱动表法没有直接计算法得直观,但是效率却比直接计算法要高那么如何实现呢?已经知道直接计算法是一步一步从上往下来异或得到得结果,在算得过程中会有异或许多生成项,而生成项又是不变的,那么是不是可以提前计算出与数据前几位符合的生成项之和然后再异或呢?
那么就将 0000 0000 ~ 1111 1111 这个范围的所有生成项计算出来存储为表格,计算的时候取数据的首字节进行索引找到表中对应生成项异或的和与去掉首字节的数据进行异或就行了。
表的形成
终于过度到表了,这里来用算法实现表,可清楚明白它的原理,这里拿 CRC32 表的形成举例首先得了解一下 CRC32 的生成项是什么
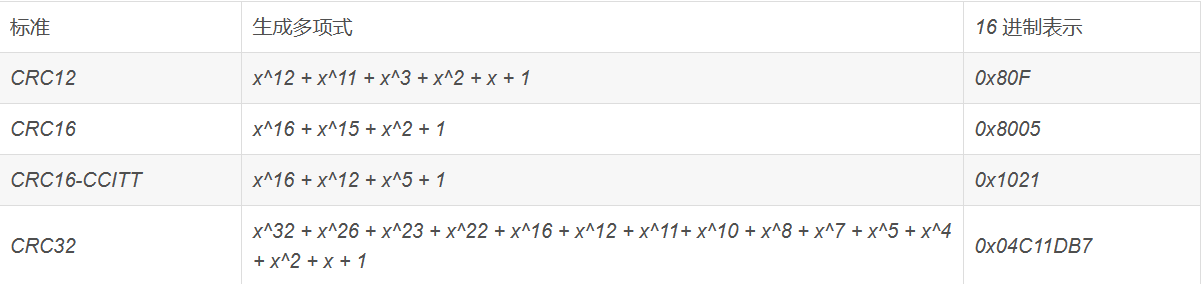
想要了解更多的 CRC 以及它的生成多项式可以去此处查看。
#include <windows.h>
#include <stdio.h>
int main(){
DWORD crc;
for (DWORD i = 0; i < 256; i++)//256个元素
{
crc = i;
for (DWORD k = 0; k < 8; k++)//因为这里异或是从数据的高位开始,所以需要计算的数据左移8位,这里就需要计算8次
{
if (crc & 1)//判断最高位是否为1
crc = (crc >> 1) ^ 0xEDB88320;//最高位为1,右移一位,然后与0xEDB88320异或
else
crc = crc >> 1;//最高位为0时,不用异或,整体数据右移一位。相当于例子2中110与000异或值是不变的
}
printf ("0x%08x, ", crc);
if (((i+1)%6) == NULL )
printf ("\n");
}
}
/*CRC32表
0x00000000, 0x77073096, 0xee0e612c, 0x990951ba, 0x076dc419, 0x706af48f,
0xe963a535, 0x9e6495a3, 0x0edb8832, 0x79dcb8a4, 0xe0d5e91e, 0x97d2d988,
0x09b64c2b, 0x7eb17cbd, 0xe7b82d07, 0x90bf1d91, 0x1db71064, 0x6ab020f2,
0xf3b97148, 0x84be41de, 0x1adad47d, 0x6ddde4eb, 0xf4d4b551, 0x83d385c7,
0x136c9856, 0x646ba8c0, 0xfd62f97a, 0x8a65c9ec, 0x14015c4f, 0x63066cd9,
0xfa0f3d63, 0x8d080df5, 0x3b6e20c8, 0x4c69105e, 0xd56041e4, 0xa2677172,
0x3c03e4d1, 0x4b04d447, 0xd20d85fd, 0xa50ab56b, 0x35b5a8fa, 0x42b2986c,
0xdbbbc9d6, 0xacbcf940, 0x32d86ce3, 0x45df5c75, 0xdcd60dcf, 0xabd13d59,
0x26d930ac, 0x51de003a, 0xc8d75180, 0xbfd06116, 0x21b4f4b5, 0x56b3c423,
0xcfba9599, 0xb8bda50f, 0x2802b89e, 0x5f058808, 0xc60cd9b2, 0xb10be924,
0x2f6f7c87, 0x58684c11, 0xc1611dab, 0xb6662d3d, 0x76dc4190, 0x01db7106,
0x98d220bc, 0xefd5102a, 0x71b18589, 0x06b6b51f, 0x9fbfe4a5, 0xe8b8d433,
0x7807c9a2, 0x0f00f934, 0x9609a88e, 0xe10e9818, 0x7f6a0dbb, 0x086d3d2d,
0x91646c97, 0xe6635c01, 0x6b6b51f4, 0x1c6c6162, 0x856530d8, 0xf262004e,
0x6c0695ed, 0x1b01a57b, 0x8208f4c1, 0xf50fc457, 0x65b0d9c6, 0x12b7e950,
0x8bbeb8ea, 0xfcb9887c, 0x62dd1ddf, 0x15da2d49, 0x8cd37cf3, 0xfbd44c65,
0x4db26158, 0x3ab551ce, 0xa3bc0074, 0xd4bb30e2, 0x4adfa541, 0x3dd895d7,
0xa4d1c46d, 0xd3d6f4fb, 0x4369e96a, 0x346ed9fc, 0xad678846, 0xda60b8d0,
0x44042d73, 0x33031de5, 0xaa0a4c5f, 0xdd0d7cc9, 0x5005713c, 0x270241aa,
0xbe0b1010, 0xc90c2086, 0x5768b525, 0x206f85b3, 0xb966d409, 0xce61e49f,
0x5edef90e, 0x29d9c998, 0xb0d09822, 0xc7d7a8b4, 0x59b33d17, 0x2eb40d81,
0xb7bd5c3b, 0xc0ba6cad, 0xedb88320, 0x9abfb3b6, 0x03b6e20c, 0x74b1d29a,
0xead54739, 0x9dd277af, 0x04db2615, 0x73dc1683, 0xe3630b12, 0x94643b84,
0x0d6d6a3e, 0x7a6a5aa8, 0xe40ecf0b, 0x9309ff9d, 0x0a00ae27, 0x7d079eb1,
0xf00f9344, 0x8708a3d2, 0x1e01f268, 0x6906c2fe, 0xf762575d, 0x806567cb,
0x196c3671, 0x6e6b06e7, 0xfed41b76, 0x89d32be0, 0x10da7a5a, 0x67dd4acc,
0xf9b9df6f, 0x8ebeeff9, 0x17b7be43, 0x60b08ed5, 0xd6d6a3e8, 0xa1d1937e,
0x38d8c2c4, 0x4fdff252, 0xd1bb67f1, 0xa6bc5767, 0x3fb506dd, 0x48b2364b,
0xd80d2bda, 0xaf0a1b4c, 0x36034af6, 0x41047a60, 0xdf60efc3, 0xa867df55,
0x316e8eef, 0x4669be79, 0xcb61b38c, 0xbc66831a, 0x256fd2a0, 0x5268e236,
0xcc0c7795, 0xbb0b4703, 0x220216b9, 0x5505262f, 0xc5ba3bbe, 0xb2bd0b28,
0x2bb45a92, 0x5cb36a04, 0xc2d7ffa7, 0xb5d0cf31, 0x2cd99e8b, 0x5bdeae1d,
0x9b64c2b0, 0xec63f226, 0x756aa39c, 0x026d930a, 0x9c0906a9, 0xeb0e363f,
0x72076785, 0x05005713, 0x95bf4a82, 0xe2b87a14, 0x7bb12bae, 0x0cb61b38,
0x92d28e9b, 0xe5d5be0d, 0x7cdcefb7, 0x0bdbdf21, 0x86d3d2d4, 0xf1d4e242,
0x68ddb3f8, 0x1fda836e, 0x81be16cd, 0xf6b9265b, 0x6fb077e1, 0x18b74777,
0x88085ae6, 0xff0f6a70, 0x66063bca, 0x11010b5c, 0x8f659eff, 0xf862ae69,
0x616bffd3, 0x166ccf45, 0xa00ae278, 0xd70dd2ee, 0x4e048354, 0x3903b3c2,
0xa7672661, 0xd06016f7, 0x4969474d, 0x3e6e77db, 0xaed16a4a, 0xd9d65adc,
0x40df0b66, 0x37d83bf0, 0xa9bcae53, 0xdebb9ec5, 0x47b2cf7f, 0x30b5ffe9,
0xbdbdf21c, 0xcabac28a, 0x53b39330, 0x24b4a3a6, 0xbad03605, 0xcdd70693,
0x54de5729, 0x23d967bf, 0xb3667a2e, 0xc4614ab8, 0x5d681b02, 0x2a6f2b94,
0xb40bbe37, 0xc30c8ea1, 0x5a05df1b, 0x2d02ef8d
*/
注意这里用红色标识的右移,这里如果按照直接计算法来说不应该是要左移吗,为什么又右移了呢?
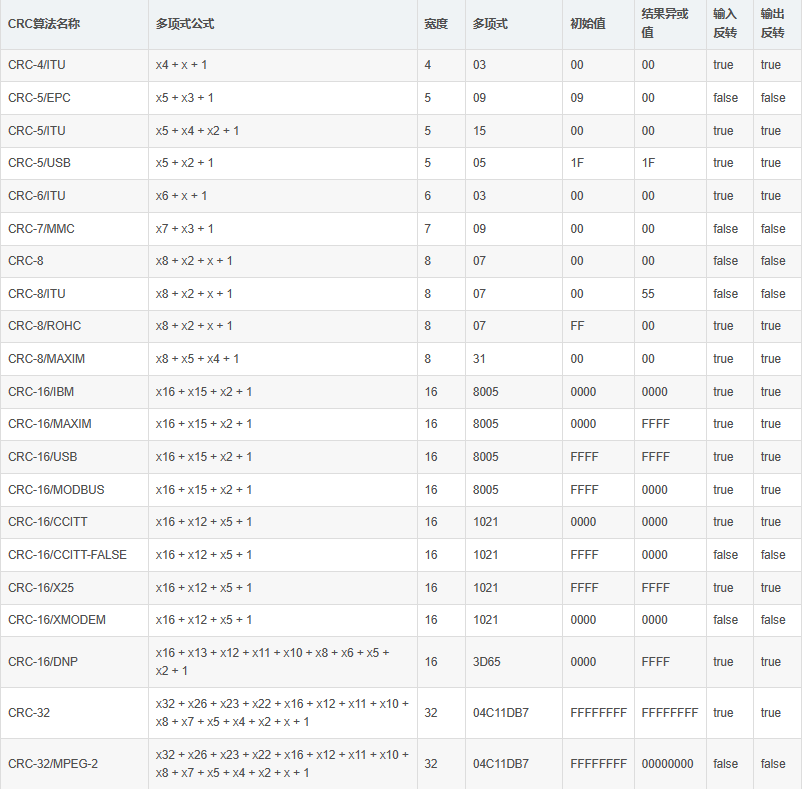
注意看这个表的倒数第二个,CRC32,它的输入和输出都是需要进行反转的,也就是相当于逆向,就要将左移修改成右移。
当然还会有人问它的多项式不应该是 0x04C11DB7 吗,怎么又变成了 0xEDB88320 了呢?
这是它是因为 0xEDB88320 是 0x04C11DB7 的反转。这个表的生成很简单,一般是用的是 0xEDB88320 这个反转多项式,假如用 0x04C11DB7 这个正常多项式则必须还要交换位,显然会很麻烦。
一个 CRC 的检测程序
相信大家差不多能够理解 CRC 实现的大概过程了,而真正需要深入了解的是 CRC32;CRC32 常用于游戏以及一些 ARJ、LHA 等压缩工具软件,那么接下来写一个 CRC32 的检测程序。
#include <windows.h>
#include <stdio.h>
DWORD crc32_table[256];
void CRC32_Table(){
DWORD crc;
//DWORD crc32_table[256];
for (int i = 0; i < 256; i++){
crc = i;
for (DWORD k = 0; k < 8; k++){
if (crc & 1)
crc = (crc >> 1) ^ 0xEDB88320;
else
crc >>= 1;
}
crc32_table[i] = crc; //生成并存储CRC32数据表
}
}
//根据CRC32表计算CRC校验码
DWORD Check_CRC32(DWORD crc, PUCHAR Data, DWORD len){
crc = 0xFFFFFFFF; //将CRC初始化为-1
CRC32_Table();
for (DWORD i = 0; i < len; i++){
crc = (crc >> 8) ^ crc32_table[(crc ^ Data[i]) & 0xff];
}
return ~crc;//输出的反转
}
int main(){
SetConsoleTitle("CRC32检测器");
printf("开始检测");
//初始内存校验值
DWORD Original_CRC32 = Check_CRC32(0, (PUCHAR)0x400000, 0x112000);
while (1){
//CRC循环校验实现实时检测
DWORD Cycle_CRC32 = Check_CRC32(0, (PUCHAR)0x400000, 0x112000);//这里第二个参数是基址,第三个个参数是一个校验的范围,也就是程序主模块镜像大小。
if (Cycle_CRC32 != Original_CRC32){
MessageBoxA(NULL, "已检测到您修改了代码!", "警告", MB_YESNO);
}
//为了防止频繁弹出信息框,这里使用的Sleep函数控制检测的周期,每5s弹出一次
Sleep(5000);
}
getchar();
}

这里初始化是因为待测数据的内容和长度是随机的,如果寄存器初始值为 0,那么待测字节是 1 字节的 0x00,与待测字节是 N 字节的 0x00,计算出来的 CRC32 值都是 0,那 CRC 值就没有意义了!所以寄存器用 0xFFFFFFFF 进行初始化,就可以避免这个问题了。
CRC校验算法分类
CRC(Cyclic Redundancy Check)校验算法是一种基于多项式除法的错误检测方法,用于数据传输和存储中的完整性验证。CRC算法的分类主要依据生成多项式的长度和特性,这些差异导致了CRC校验码的不同长度和错误检测能力。CRC16、CRC32、CRC8等都是根据生成多项式的位数命名的,分别表示16位、32位和8位的校验码长度。
CRC校验算法分类的情况:
CRC8:生成的校验码长度为8位(1字节)。它通常用于小数据量的校验,比如在一些简单的通信协议中,或者是对字节级数据进行校验。由于校验码长度较短,CRC8的冲突概率较高,但是计算速度非常快。
CRC16:生成的校验码长度为16位(2字节)。它适用于中等大小的数据块校验,例如在串行通信中或者对短消息进行校验。CRC16的冲突概率比CRC8低,但仍然存在一定的可能性,尤其是在校验较长的数据流时。
CRC32:生成的校验码长度为32位(4字节)。它是最常见的CRC算法,适用于对大型数据块、文件或者网络数据包进行校验。CRC32提供了更高级别的错误检测能力,冲突率极低,适合于需要高度可靠性的数据传输场景。计算CRC32虽然相对于CRC16和CRC8要稍微慢一些,但由于现代处理器的速度,这种差异在实际应用中往往可以忽略。
除了上述常见的CRC版本,还有CRC64,生成64位的校验码,适用于要求极高可靠性的应用中。
为什么有CRC16、CRC32等不同版本?
不同版本的CRC校验算法之所以存在,主要是为了平衡错误检测能力和计算效率。在某些情况下,可能不需要过于强大的错误检测能力,例如在短距离、低噪声环境下的通信,这时使用CRC8或CRC16就足够了,因为它们计算速度快,硬件实现简单,可以节省资源。然而,在长距离、高噪声环境下,或者在需要高度可靠性的数据传输中,比如互联网数据包的传输,CRC32或CRC64就是更好的选择,因为它们可以检测到更多类型的错误,尽管计算成本会相应增加。
在不同的应用领域可能有各自的标准和要求,比如在某些通信协议中,CRC16的特定变体(如CRC-CCITT、CRC-16/ARC)是被规定的,而在其他地方,比如压缩文件和网络传输中,CRC32可能是首选。CRC16、CRC32等不同版本的CRC校验算法是为了适应不同应用场景的需求,它们在错误检测能力和计算效率之间提供了不同的权衡。
查表法
在CRC(Cyclic Redundancy Check)算法的实现中,经常使用一个预计算的查找表(lookup table),这个查找表就是一个数组,用来加速CRC的计算过程。这个数组通常被称为“CRC表”或“CRC查找表”。CRC算法的核心是基于二进制的多项式除法,其中使用的除数是一个固定的多项式(即生成多项式)。在软件实现中,特别是当需要快速计算CRC校验值时,查找表可以显著减少计算量。查找表的工作原理:
1.预计算: 在CRC算法的初始化阶段,程序会预先计算出所有可能的8位(或其他位数,取决于查找表的设计)输入与生成多项式进行模2除法的结果,并将这些结果存储在一个数组中。这个数组的大小通常是256个元素,每个元素对应一个8位输入的CRC校验值。
2.快速计算: 当实际计算数据的CRC校验值时,算法会对数据进行逐字节处理。对于每个字节,算法会在查找表中查找对应的CRC值,然后与之前计算得到的部分CRC值进行异或操作。这个过程会重复直到所有的数据字节都被处理完毕。
3.最终CRC值: 在处理完所有数据后,累积的CRC值会经过可能的反转(reflect)和初始值(seed)调整,得到最终的CRC校验值。
使用查找表的主要优点是减少了每次迭代中的复杂计算,尤其是避免了多项式除法,而代之以简单的数组查找和异或操作,这在大多数现代计算机架构上是非常快速的。
查找表的生成:查找表的生成涉及对每一个可能的8位输入(从0到255)执行CRC算法的完整计算过程,并存储最终结果。这个过程只在程序启动时执行一次,之后就可以复用这个查找表来快速计算任何数据的CRC校验值。查找表的使用使得CRC计算在软件中变得既快速又高效,尤其在实时系统和大量数据处理中,这一点尤为重要。
代码实操
文件校验-CRC8
下面是一个使用C语言实现的CRC8校验值计算的示例代码。这里使用一个常见的生成多项式 0x07(也就是多项式 x^8 + x^2 + x^1 + x^0)来生成CRC8校验和。 使用一个查找表来优化计算过程。
#include <stdio.h>
#include <stdint.h>
#include <fcntl.h>
#include <unistd.h>
// CRC8生成多项式
#define POLYNOMIAL 0x07
// 初始化CRC8查找表
uint8_t crc8_table[256];
void init_crc8_table(void) {
uint8_t i, j;
for (i = 0; i < 256; i++) {
uint8_t crc = i;
for (j = 8; j; j--) {
if (crc & 0x80)
crc = (crc << 1) ^ POLYNOMIAL;
else
crc <<= 1;
}
crc8_table[i] = crc;
}
}
uint8_t crc8(const void *data, size_t len) {
const uint8_t *byte = data;
uint8_t crc = 0x00;
for (; len > 0; len--) {
crc = crc8_table[(crc ^ *byte++) & 0xFF];
}
return crc;
}
int main(int argc, char *argv[]) {
int fd;
uint8_t buffer[4096];
size_t bytes_read;
uint8_t crc;
if (argc != 2) {
fprintf(stderr, "Usage: %s filename\n", argv[0]);
return 1;
}
// 初始化CRC8查找表
init_crc8_table();
// 打开文件
fd = open(argv[1], O_RDONLY);
if (fd == -1) {
perror("Error opening file");
return 1;
}
// 读取文件并计算CRC8校验值
crc = 0x00;
while ((bytes_read = read(fd, buffer, sizeof(buffer))) > 0) {
crc = crc8(buffer, bytes_read);
}
close(fd);
// 输出CRC8校验值
printf("CRC8 checksum: 0x%02X\n", crc);
return 0;
}
这段代码首先定义了一个CRC8查找表,并通过init_crc8_table函数进行初始化。crc8函数用于计算给定数据块的CRC8校验值,它使用查找表来进行快速计算。main函数负责打开文件、读取数据并调用crc8函数来计算整个文件的CRC8校验值。
文件校验-CRC16
下面是使用CRC16并采用CCITT标准生成多项式(0x1021,即多项式x^16 + x^12 + x^5 + x^0)来计算文件CRC16校验值的C语言代码示例。与之前的CRC8示例类似,这里也会使用查找表来优化计算过程。
#include <stdio.h>
#include <stdint.h>
#include <fcntl.h>
#include <unistd.h>
// CRC16 CCITT生成多项式
#define POLYNOMIAL 0x1021
// 初始化CRC16查找表
uint16_t crc16_table[256];
void init_crc16_table(void) {
uint16_t crc, poly;
uint8_t i, j;
for (i = 0; i < 256; i++) {
crc = i;
for (j = 8; j; j--) {
if (crc & 0x0001)
crc = (crc >> 1) ^ POLYNOMIAL;
else
crc >>= 1;
}
crc16_table[i] = crc;
}
}
uint16_t crc16(const void *data, size_t len) {
const uint8_t *byte = data;
uint16_t crc = 0xFFFF;
while (len--) {
crc = (crc >> 8) ^ crc16_table[(crc ^ *byte++) & 0xFF];
}
return crc;
}
int main(int argc, char *argv[]) {
int fd;
uint8_t buffer[4096];
size_t bytes_read;
uint16_t crc;
if (argc != 2) {
fprintf(stderr, "Usage: %s filename\n", argv[0]);
return 1;
}
// 初始化CRC16查找表
init_crc16_table();
// 打开文件
fd = open(argv[1], O_RDONLY);
if (fd == -1) {
perror("Error opening file");
return 1;
}
// 读取文件并计算CRC16校验值
crc = 0xFFFF;
while ((bytes_read = read(fd, buffer, sizeof(buffer))) > 0) {
crc = crc16(buffer, bytes_read);
}
close(fd);
// 输出CRC16校验值
printf("CRC16 checksum: 0x%04X\n", crc);
return 0;
}
这个示例代码中的init_crc16_table函数用于生成CRC16的查找表,而crc16函数则利用该表计算输入数据的CRC16校验值。在主函数main中,程序会读取文件的内容并调用crc16函数计算CRC16校验值,最后输出该值。
文件校验-CRC32
下面是一个使用CRC32算法计算文件校验和的C语言代码示例。这里使用的是IEEE 802.3标准的多项式(0x04C11DB7),这是最常用的CRC32实现。
#include <stdio.h>
#include <stdint.h>
#include <fcntl.h>
#include <unistd.h>
// CRC32 IEEE 802.3生成多项式
#define POLYNOMIAL 0xEDB88320
// 初始化CRC32查找表
uint32_t crc32_table[256];
void init_crc32_table(void) {
uint32_t crc, poly;
uint8_t i, j;
for (i = 0; i < 256; i++) {
crc = i;
for (j = 8; j; j--) {
if (crc & 0x00000001)
crc = (crc >> 1) ^ POLYNOMIAL;
else
crc >>= 1;
}
crc32_table[i] = crc;
}
}
uint32_t crc32(const void *data, size_t len) {
const uint8_t *byte = data;
uint32_t crc = 0xFFFFFFFF;
while (len--){
crc = (crc >> 8) ^ crc32_table[(crc ^ *byte++) & 0xFF];
}
return crc ^ 0xFFFFFFFF;
}
int main(int argc, char *argv[]) {
int fd;
uint8_t buffer[4096];
size_t bytes_read;
uint32_t crc;
if (argc != 2) {
fprintf(stderr, "Usage: %s filename\n", argv[0]);
return 1;
}
// 初始化CRC32查找表
init_crc32_table();
// 打开文件
fd = open(argv[1], O_RDONLY);
if (fd == -1) {
perror("Error opening file");
return 1;
}
// 读取文件并计算CRC32校验值
crc = 0xFFFFFFFF;
while ((bytes_read = read(fd, buffer, sizeof(buffer))) > 0) {
crc = crc32(buffer, bytes_read);
}
close(fd);
// 输出CRC32校验值
printf("CRC32 checksum: 0x%08X\n", crc);
return 0;
}
在这个示例中,init_crc32_table函数初始化了CRC32的查找表,crc32函数用于计算输入数据的CRC32校验值。主函数main负责读取文件内容并调用crc32函数计算CRC32校验值,最后输出该值。
注意,在CRC32计算结束时,通常需要对CRC值进行反转(XOR 0xFFFFFFFF),这是为了与大多数CRC32实现保持一致。
因而在数据存储和数据通讯领域,CRC无处不在:著名的通讯协议X.25的FCS(帧检错序列)采用的是CRC-CCITT,ARJ、LHA等压缩工具软件采用的是CRC32,磁盘驱动器的读写采用了CRC16,通用的图像存储格式GIF、TIFF等也都用CRC作为检错手段。简而言之,CRC是一个数值。该数值被用于校验数据的正确性。CRC数值简单地说就是通过让你需要做处理的数据除以一个常数而得到的余数。当你得到这个数值后你可以将这个数值附加到你的数据后,当数据被传送到其他地方后,取出原始数据(可能在传送过程中被破坏)与附加的CRC数值,然后将这里的原始数据除以之前那个常数(约定好的)然后得到新的CRC值。比较两个CRC值是否相等即可确认你的数据是否在传送过程中出现错误。
那么如何让数据除以一个常数?方法是对你的数据进行必要的编码处理,逐字节处理成数字。那么这个常数是什么?你不必关注它是什么,也不需要关注它是如何获得的。当你真的要动手写一个CRC的实现算法时,我可以告诉你,CRC的理论学家会告诉你。不同长度的常数对应着不同的CRC实现算法。当这个常数为32位时,也就是这里所说的CRC32。
CRC的本质是模-2除法的余数,采用的除数不同,CRC的类型也就不一样。通常,CRC的除数用生成多项式来表示。由于CRC在通讯和数据处理软件中经常采用,笔者在实际工作中对其算法进行了研究和比较,总结并编写了一个具有最高效率的CRC通用程序库。该程序采用查表法计算CRC,在速度上优于一般的直接模仿硬件的算法,可以应用于通讯和数据压缩程序。因此很多教科书会把CRC与多项式关联起来。这里的多项式指的是系数为0或1的式子,例如:a0 + a1*x + a2*x^2 + ... + an*x^n。其中a0, a1, ..., an要么为0要么为1。我们并不关注x取什么值。(如果你要关注,你可以简单地认为x为2) 这里把a0, a1, ..., an的值取出来排列起来,就可以表示比特流。例如 1 + x + x^3所表示的比特流就为:1101。部分资料会将这个顺序颠倒,这个很正常。
通常的CRC算法在计算一个数据段的CRC值时,其CRC值是由求解每个数值的CRC值的和对CRC寄存器的值反复更新而得到的。这样求解CRC的速度较慢。通过对CRC算法的研究,我们发现:一个8位数据加到16位累加器中去,只有累加器的高8位或低8位与数据相作用,其结果仅有256种可能的组合值。因而我们可以用查表法来代替反复的运算,这也同样适用于CRC32的计算。
CRC算法通过计算一个固定长度的校验码,将该校验码附加到原始数据的末尾,接收方在接收到数据后重新计算校验码并与接收到的校验码进行比较,以此判断数据在传输过程中是否发生了错误。这种校验机制不仅能够检测出大多数类型的错误,而且计算效率高,占用资源少,因此在各种通信协议、文件系统、磁盘驱动器和网络协议中都有广泛应用。其原理基于多项式除法。在CRC校验中,数据被视为一个系数为0或1的多项式序列,而CRC校验码则是通过使用一个预定义的生成多项式对该数据多项式进行模2除法运算得到的。生成多项式的选择对CRC算法的错误检测能力有重要影响,通常选取的生成多项式能够检测出尽可能多类型的错误。在计算CRC校验码时,原始数据与生成多项式的模2除法的结果被附加到数据的末尾,形成一个完整的数据包。在接收端,同样使用生成多项式对数据包进行模2除法,如果余数为零,则认为数据在传输过程中未发生错误。
具体实现过程如下:
1.将待发送的数据视为一个二进制多项式D(x),其中每一位代表一个系数。
2.选取一个生成多项式G(x),该多项式的长度决定了CRC校验码的长度。
3.对D(x)乘以x^n(n为生成多项式的长度减1),形成一个与G(x)同阶的多项式。
4.使用生成多项式G(x)对该扩展后的多项式进行模2除法,得到的余数即为CRC校验码。
5.将CRC校验码附加到原始数据的末尾,形成完整的数据包。
6.在接收端,对数据包再次进行相同的模2除法运算,若余数为零,则认为数据包未发生错误。
CRC校验算法在实际应用中非常灵活,可以通过选择不同的生成多项式来适应不同场合的需求。例如,CRC-32使用一个32位的生成多项式,可以检测出绝大多数常见的错误类型,包括所有奇数位错误、所有双位错误(在数据长度不超过31位的情况下)、所有突发错误(长度小于等于32位)以及大多数长度超过32位的突发错误。
在C语言中实现CRC算法时,可以利用位运算和循环结构来高效地完成模2除法运算。下面是使用标准C库函数和位运算符来实现CRC-32算法示例:
#include <stdint.h>
uint32_t crc32(const unsigned char *buf, size_t len) {
uint32_t crc = 0xFFFFFFFF;
const unsigned char *end = buf + len;
uint32_t table[256];
// Pre-compute the CRC table
for (int i = 0; i < 256; i++) {
uint32_t c = i;
for (int j = 0; j < 8; j++) {
if (c & 1) {
c = 0xEDB88320 ^ (c >> 1);
} else {
c = c >> 1;
}
}
table[i] = c;
}
// Process each byte of the data
while (buf < end) {
crc = table[(crc ^ *buf++) & 0xFF] ^ (crc >> 8);
}
return crc ^ 0xFFFFFFFF;
}
这段代码首先预计算了一个CRC表,用于加速后续的模2除法运算,然后逐字节处理输入数据,最终返回CRC校验码。通过这种方式,CRC算法能在保证准确性的同时,达到较高的计算速度,满足实时性和效率的要求。CRC校验算法凭借其高效的错误检测能力,在数据通信和存储系统中发挥着不可或缺的作用。无论是嵌入式系统、网络通信还是文件系统,CRC都是确保数据完整性和可靠性的一种重要手段。
什么是生成多项式?
所谓的生成多项式,就是上面我所说的常数。注意,在这里,一个多项式就表示了一个比特流,也就是一堆1、0,组合起来最终就是一个数值。例如CRC32算法中,这个生成多项式为:c(x) = 1 + x + x^2 + x^4 + x^5 + x^7 + x^8 + x^10 + x^11 + x^12 + x^16 + x^22 + x^23 + x^26 + x^32。
其对应的数字就为:11101101101110001000001100100000(x^32在实际计算时隐含给出,因此这里没有包含它的系数),也就是0xEDB88320(多项式对应的数字可能颠倒,颠倒后得到的是0x04C11DB7,其实也是正确的)。 由此可以看出,CRC值也可以看成我们的数据除以一个生成多项式而得到的余数。
如何做这个除法?
套用大部分教科书给出的计算方法,因为任何数据都可以被处理成纯数字,因此,在某种程度上说,我们可以直接开始这个除法。尽管事实上这并不是标准的除法。例如,我们的数据为1101011011(方便起见我直接给二进制表示了,从这里也可以看出,CRC是按bit进行计算的),给定的生成多项式(对应的值)为10011。通常的教科书会告诉我们在进行这个除法前,会把我们的数据左移几位(生成多项式位数-1位),从而可以容纳将来计算得到的CRC值(我上面所说的将CRC值附加到原始数据后)。但是为什么要这样做?我也不知道(不知道的东西不能含糊而过)。那么,除法就为:
1100001010
_______________
10011 ) 11010110110000 附加了几个零的新数据
10011......... 这里的减法(希望你不至于忘掉小学算术)是一个异或操作
-----.........
10011........
10011........
-----........
00001....... 逐bit计算
00000.......
-----.......
00010......
00000......
-----......
00101.....
00000.....
-----.....
01011....
00000....
-----....
10110...
10011...
-----...
01010..
00000..
-----..
10100.
10011.
-----.
01110
00000
-----
1110 = 这个余数也就是所谓的CRC值,通常又被称为校验值。
希望进行到这里,你可以获取更多关于CRC的感性认识。而我们所要做的,也就是实现一个CRC的计算算法。说白了,就是提供一个程序,给定一段数据,以及一个生成多项式(对于CRC32算法而言该值固定),然后计算得出上面的1110余数。
CRC32算法冲突概率

1)、CRC32在完全随机的输入情况下,冲突概率还是比较高的,特别是到了1亿的数据量后,冲突概率会更高。
2)、CRC32在输入某个连续段的数据情况下,冲突概率反而很低,这是因为两个冲突的原值理论上应该是相隔很远,只输入某段数据的情况下,这个段里面冲突的原值会很少。
上文对CRC进行了简略的介绍,接下来对其进行较为详细的讲解,并提供一些代码实现。CRC 也叫循环冗余校验码,它属于密码学一类算法,常用于数据校验,一般会用来检测程序是否被脱壳或者被修改,以达到防破解的目的。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。CRC 运算实际上就是将数据 k 进行模 2 运算,得到余数 n,然后将 n 拼接到 k 的后面生成 k+n 为循环冗余校验码的字长。接着发送 k+n 到接收方作为被除数进行模 2 运算,判断余数是否为 0,如果余数非 0 则 CRC 检测出数据被修改了。简单点说就是把需要校验的数据与生成多项式进行循环异或处理:
1.发送方和接受方会约定一个特定的除数,它是一个定值,我们也叫除数为生成多项式;
2.在计算余数时,被除数也就是数据 k 需要进行补 0,补 0 个数为生成多项式长度 - 1 个 0;
3.余数长度一定与补零的长度一致。
流程图:

示例如下
例1:这里数据为 1110101,生成多项式为 101,那么我们要传给接收方的数据就为 1110101(数据)+10(余数)=111010110

这个就是 CRC 的计算原理了,其算法参数模型解释:
NAME:参数模型名称。
WIDTH:宽度,即CRC比特数。
POLY:生成项的简写,以16进制表示。例如:CRC-32即是0x04C11DB7,忽略了最高位的"1",即完整的生成项是0x104C11DB7。
INIT:这是算法开始时寄存器(crc)的初始化预置值,十六进制表示。
REFIN:待测数据的每个字节是否按位反转,True或False。
REFOUT:在计算后之后,异或输出之前,整个数据是否按位反转,True或False。
XOROUT:计算结果与此参数异或后得到最终的CRC值。
CRC 计算的两种方式
1. 直接计算法
这里通过例子来讲解,例2:

首先看到这里的生成项是 1101,然后在计算中的除数(蓝色字体标记)大多是 1101 而有时是 0000,当除数为 1101 时被除数的首位都是 1,而首位不为 1 时就是 0000。那么不妨做个假设,既然被除数和除数的首位为 1 时会被消掉那么我们就不需要四位异或了,改成三位异或,三位异或的话被除数一次就取三个,而除数取后三个,当被除数首位为 1 时就左移一位让新的三位与除数(生成项)的后三位进行异或;当被除数移出位是 0 时就异或 000,然后不断重复此步骤直至结束。(这里是针对本例题的,当你的生成项为 n 时,你就取 n-1 位异或)
那么就会有人问到底需要重复几次才算结束呢?
处理次数 = 待处理数据位数(被除数位数)= 商的位数(本题次数为 6 次)
例如本题第一次被除数取 100,左移一位得 001 然后与 101 异或得 100。100 左移一位得 000 然后与 101 异或得 101。101 左移一位得 010 然后与 101 异或得 111。111 左移一位得 110 然后与 101 异或得 011。011 左移一位得 110 然后与 000 异或得 110(与 000 异或值是不变的)。110 左移一位得 100 然后与 101 异或得 001 得到余数刚好 6 次。
2. 驱动表法
驱动表法没有直接计算法得直观,但是效率却比直接计算法要高那么如何实现呢?已经知道直接计算法是一步一步从上往下来异或得到得结果,在算得过程中会有异或许多生成项,而生成项又是不变的,那么是不是可以提前计算出与数据前几位符合的生成项之和然后再异或呢?
那么就将 0000 0000 ~ 1111 1111 这个范围的所有生成项计算出来存储为表格,计算的时候取数据的首字节进行索引找到表中对应生成项异或的和与去掉首字节的数据进行异或就行了。
表的形成
终于过度到表了,这里来用算法实现表,可清楚明白它的原理,这里拿 CRC32 表的形成举例首先得了解一下 CRC32 的生成项是什么
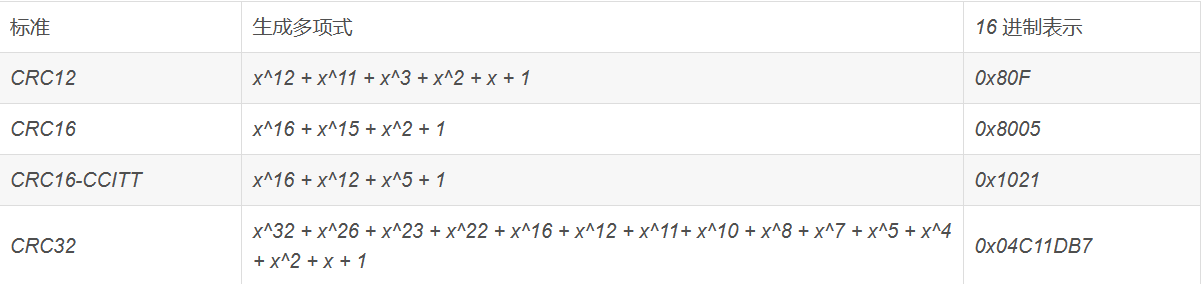
想要了解更多的 CRC 以及它的生成多项式可以去此处查看。
#include <windows.h>
#include <stdio.h>
int main(){
DWORD crc;
for (DWORD i = 0; i < 256; i++)//256个元素
{
crc = i;
for (DWORD k = 0; k < 8; k++)//因为这里异或是从数据的高位开始,所以需要计算的数据左移8位,这里就需要计算8次
{
if (crc & 1)//判断最高位是否为1
crc = (crc >> 1) ^ 0xEDB88320;//最高位为1,右移一位,然后与0xEDB88320异或
else
crc = crc >> 1;//最高位为0时,不用异或,整体数据右移一位。相当于例子2中110与000异或值是不变的
}
printf ("0x%08x, ", crc);
if (((i+1)%6) == NULL )
printf ("\n");
}
}
/*CRC32表
0x00000000, 0x77073096, 0xee0e612c, 0x990951ba, 0x076dc419, 0x706af48f,
0xe963a535, 0x9e6495a3, 0x0edb8832, 0x79dcb8a4, 0xe0d5e91e, 0x97d2d988,
0x09b64c2b, 0x7eb17cbd, 0xe7b82d07, 0x90bf1d91, 0x1db71064, 0x6ab020f2,
0xf3b97148, 0x84be41de, 0x1adad47d, 0x6ddde4eb, 0xf4d4b551, 0x83d385c7,
0x136c9856, 0x646ba8c0, 0xfd62f97a, 0x8a65c9ec, 0x14015c4f, 0x63066cd9,
0xfa0f3d63, 0x8d080df5, 0x3b6e20c8, 0x4c69105e, 0xd56041e4, 0xa2677172,
0x3c03e4d1, 0x4b04d447, 0xd20d85fd, 0xa50ab56b, 0x35b5a8fa, 0x42b2986c,
0xdbbbc9d6, 0xacbcf940, 0x32d86ce3, 0x45df5c75, 0xdcd60dcf, 0xabd13d59,
0x26d930ac, 0x51de003a, 0xc8d75180, 0xbfd06116, 0x21b4f4b5, 0x56b3c423,
0xcfba9599, 0xb8bda50f, 0x2802b89e, 0x5f058808, 0xc60cd9b2, 0xb10be924,
0x2f6f7c87, 0x58684c11, 0xc1611dab, 0xb6662d3d, 0x76dc4190, 0x01db7106,
0x98d220bc, 0xefd5102a, 0x71b18589, 0x06b6b51f, 0x9fbfe4a5, 0xe8b8d433,
0x7807c9a2, 0x0f00f934, 0x9609a88e, 0xe10e9818, 0x7f6a0dbb, 0x086d3d2d,
0x91646c97, 0xe6635c01, 0x6b6b51f4, 0x1c6c6162, 0x856530d8, 0xf262004e,
0x6c0695ed, 0x1b01a57b, 0x8208f4c1, 0xf50fc457, 0x65b0d9c6, 0x12b7e950,
0x8bbeb8ea, 0xfcb9887c, 0x62dd1ddf, 0x15da2d49, 0x8cd37cf3, 0xfbd44c65,
0x4db26158, 0x3ab551ce, 0xa3bc0074, 0xd4bb30e2, 0x4adfa541, 0x3dd895d7,
0xa4d1c46d, 0xd3d6f4fb, 0x4369e96a, 0x346ed9fc, 0xad678846, 0xda60b8d0,
0x44042d73, 0x33031de5, 0xaa0a4c5f, 0xdd0d7cc9, 0x5005713c, 0x270241aa,
0xbe0b1010, 0xc90c2086, 0x5768b525, 0x206f85b3, 0xb966d409, 0xce61e49f,
0x5edef90e, 0x29d9c998, 0xb0d09822, 0xc7d7a8b4, 0x59b33d17, 0x2eb40d81,
0xb7bd5c3b, 0xc0ba6cad, 0xedb88320, 0x9abfb3b6, 0x03b6e20c, 0x74b1d29a,
0xead54739, 0x9dd277af, 0x04db2615, 0x73dc1683, 0xe3630b12, 0x94643b84,
0x0d6d6a3e, 0x7a6a5aa8, 0xe40ecf0b, 0x9309ff9d, 0x0a00ae27, 0x7d079eb1,
0xf00f9344, 0x8708a3d2, 0x1e01f268, 0x6906c2fe, 0xf762575d, 0x806567cb,
0x196c3671, 0x6e6b06e7, 0xfed41b76, 0x89d32be0, 0x10da7a5a, 0x67dd4acc,
0xf9b9df6f, 0x8ebeeff9, 0x17b7be43, 0x60b08ed5, 0xd6d6a3e8, 0xa1d1937e,
0x38d8c2c4, 0x4fdff252, 0xd1bb67f1, 0xa6bc5767, 0x3fb506dd, 0x48b2364b,
0xd80d2bda, 0xaf0a1b4c, 0x36034af6, 0x41047a60, 0xdf60efc3, 0xa867df55,
0x316e8eef, 0x4669be79, 0xcb61b38c, 0xbc66831a, 0x256fd2a0, 0x5268e236,
0xcc0c7795, 0xbb0b4703, 0x220216b9, 0x5505262f, 0xc5ba3bbe, 0xb2bd0b28,
0x2bb45a92, 0x5cb36a04, 0xc2d7ffa7, 0xb5d0cf31, 0x2cd99e8b, 0x5bdeae1d,
0x9b64c2b0, 0xec63f226, 0x756aa39c, 0x026d930a, 0x9c0906a9, 0xeb0e363f,
0x72076785, 0x05005713, 0x95bf4a82, 0xe2b87a14, 0x7bb12bae, 0x0cb61b38,
0x92d28e9b, 0xe5d5be0d, 0x7cdcefb7, 0x0bdbdf21, 0x86d3d2d4, 0xf1d4e242,
0x68ddb3f8, 0x1fda836e, 0x81be16cd, 0xf6b9265b, 0x6fb077e1, 0x18b74777,
0x88085ae6, 0xff0f6a70, 0x66063bca, 0x11010b5c, 0x8f659eff, 0xf862ae69,
0x616bffd3, 0x166ccf45, 0xa00ae278, 0xd70dd2ee, 0x4e048354, 0x3903b3c2,
0xa7672661, 0xd06016f7, 0x4969474d, 0x3e6e77db, 0xaed16a4a, 0xd9d65adc,
0x40df0b66, 0x37d83bf0, 0xa9bcae53, 0xdebb9ec5, 0x47b2cf7f, 0x30b5ffe9,
0xbdbdf21c, 0xcabac28a, 0x53b39330, 0x24b4a3a6, 0xbad03605, 0xcdd70693,
0x54de5729, 0x23d967bf, 0xb3667a2e, 0xc4614ab8, 0x5d681b02, 0x2a6f2b94,
0xb40bbe37, 0xc30c8ea1, 0x5a05df1b, 0x2d02ef8d
*/
注意这里用红色标识的右移,这里如果按照直接计算法来说不应该是要左移吗,为什么又右移了呢?

注意看这个表的倒数第二个,CRC32,它的输入和输出都是需要进行反转的,也就是相当于逆向,就要将左移修改成右移。
当然还会有人问它的多项式不应该是 0x04C11DB7 吗,怎么又变成了 0xEDB88320 了呢?
这是它是因为 0xEDB88320 是 0x04C11DB7 的反转。这个表的生成很简单,一般是用的是 0xEDB88320 这个反转多项式,假如用 0x04C11DB7 这个正常多项式则必须还要交换位,显然会很麻烦。
一个 CRC 的检测程序
相信大家差不多能够理解 CRC 实现的大概过程了,而真正需要深入了解的是 CRC32;CRC32 常用于游戏以及一些 ARJ、LHA 等压缩工具软件,那么接下来写一个 CRC32 的检测程序。
#include <windows.h>
#include <stdio.h>
DWORD crc32_table[256];
void CRC32_Table(){
DWORD crc;
//DWORD crc32_table[256];
for (int i = 0; i < 256; i++){
crc = i;
for (DWORD k = 0; k < 8; k++){
if (crc & 1)
crc = (crc >> 1) ^ 0xEDB88320;
else
crc >>= 1;
}
crc32_table[i] = crc; //生成并存储CRC32数据表
}
}
//根据CRC32表计算CRC校验码
DWORD Check_CRC32(DWORD crc, PUCHAR Data, DWORD len){
crc = 0xFFFFFFFF; //将CRC初始化为-1
CRC32_Table();
for (DWORD i = 0; i < len; i++){
crc = (crc >> 8) ^ crc32_table[(crc ^ Data[i]) & 0xff];
}
return ~crc;//输出的反转
}
int main(){
SetConsoleTitle("CRC32检测器");
printf("开始检测");
//初始内存校验值
DWORD Original_CRC32 = Check_CRC32(0, (PUCHAR)0x400000, 0x112000);
while (1){
//CRC循环校验实现实时检测
DWORD Cycle_CRC32 = Check_CRC32(0, (PUCHAR)0x400000, 0x112000);//这里第二个参数是基址,第三个个参数是一个校验的范围,也就是程序主模块镜像大小。
if (Cycle_CRC32 != Original_CRC32){
MessageBoxA(NULL, "已检测到您修改了代码!", "警告", MB_YESNO);
}
//为了防止频繁弹出信息框,这里使用的Sleep函数控制检测的周期,每5s弹出一次
Sleep(5000);
}
getchar();
}

这里初始化是因为待测数据的内容和长度是随机的,如果寄存器初始值为 0,那么待测字节是 1 字节的 0x00,与待测字节是 N 字节的 0x00,计算出来的 CRC32 值都是 0,那 CRC 值就没有意义了!所以寄存器用 0xFFFFFFFF 进行初始化,就可以避免这个问题了。
CRC校验算法分类
CRC(Cyclic Redundancy Check)校验算法是一种基于多项式除法的错误检测方法,用于数据传输和存储中的完整性验证。CRC算法的分类主要依据生成多项式的长度和特性,这些差异导致了CRC校验码的不同长度和错误检测能力。CRC16、CRC32、CRC8等都是根据生成多项式的位数命名的,分别表示16位、32位和8位的校验码长度。
CRC校验算法分类的情况:
CRC8:生成的校验码长度为8位(1字节)。它通常用于小数据量的校验,比如在一些简单的通信协议中,或者是对字节级数据进行校验。由于校验码长度较短,CRC8的冲突概率较高,但是计算速度非常快。
CRC16:生成的校验码长度为16位(2字节)。它适用于中等大小的数据块校验,例如在串行通信中或者对短消息进行校验。CRC16的冲突概率比CRC8低,但仍然存在一定的可能性,尤其是在校验较长的数据流时。
CRC32:生成的校验码长度为32位(4字节)。它是最常见的CRC算法,适用于对大型数据块、文件或者网络数据包进行校验。CRC32提供了更高级别的错误检测能力,冲突率极低,适合于需要高度可靠性的数据传输场景。计算CRC32虽然相对于CRC16和CRC8要稍微慢一些,但由于现代处理器的速度,这种差异在实际应用中往往可以忽略。
除了上述常见的CRC版本,还有CRC64,生成64位的校验码,适用于要求极高可靠性的应用中。
为什么有CRC16、CRC32等不同版本?
不同版本的CRC校验算法之所以存在,主要是为了平衡错误检测能力和计算效率。在某些情况下,可能不需要过于强大的错误检测能力,例如在短距离、低噪声环境下的通信,这时使用CRC8或CRC16就足够了,因为它们计算速度快,硬件实现简单,可以节省资源。然而,在长距离、高噪声环境下,或者在需要高度可靠性的数据传输中,比如互联网数据包的传输,CRC32或CRC64就是更好的选择,因为它们可以检测到更多类型的错误,尽管计算成本会相应增加。
在不同的应用领域可能有各自的标准和要求,比如在某些通信协议中,CRC16的特定变体(如CRC-CCITT、CRC-16/ARC)是被规定的,而在其他地方,比如压缩文件和网络传输中,CRC32可能是首选。CRC16、CRC32等不同版本的CRC校验算法是为了适应不同应用场景的需求,它们在错误检测能力和计算效率之间提供了不同的权衡。
查表法
在CRC(Cyclic Redundancy Check)算法的实现中,经常使用一个预计算的查找表(lookup table),这个查找表就是一个数组,用来加速CRC的计算过程。这个数组通常被称为“CRC表”或“CRC查找表”。CRC算法的核心是基于二进制的多项式除法,其中使用的除数是一个固定的多项式(即生成多项式)。在软件实现中,特别是当需要快速计算CRC校验值时,查找表可以显著减少计算量。查找表的工作原理:
1.预计算: 在CRC算法的初始化阶段,程序会预先计算出所有可能的8位(或其他位数,取决于查找表的设计)输入与生成多项式进行模2除法的结果,并将这些结果存储在一个数组中。这个数组的大小通常是256个元素,每个元素对应一个8位输入的CRC校验值。
2.快速计算: 当实际计算数据的CRC校验值时,算法会对数据进行逐字节处理。对于每个字节,算法会在查找表中查找对应的CRC值,然后与之前计算得到的部分CRC值进行异或操作。这个过程会重复直到所有的数据字节都被处理完毕。
3.最终CRC值: 在处理完所有数据后,累积的CRC值会经过可能的反转(reflect)和初始值(seed)调整,得到最终的CRC校验值。
使用查找表的主要优点是减少了每次迭代中的复杂计算,尤其是避免了多项式除法,而代之以简单的数组查找和异或操作,这在大多数现代计算机架构上是非常快速的。
查找表的生成:查找表的生成涉及对每一个可能的8位输入(从0到255)执行CRC算法的完整计算过程,并存储最终结果。这个过程只在程序启动时执行一次,之后就可以复用这个查找表来快速计算任何数据的CRC校验值。查找表的使用使得CRC计算在软件中变得既快速又高效,尤其在实时系统和大量数据处理中,这一点尤为重要。
代码实操
文件校验-CRC8
下面是一个使用C语言实现的CRC8校验值计算的示例代码。这里使用一个常见的生成多项式 0x07(也就是多项式 x^8 + x^2 + x^1 + x^0)来生成CRC8校验和。 使用一个查找表来优化计算过程。
#include <stdio.h>
#include <stdint.h>
#include <fcntl.h>
#include <unistd.h>
// CRC8生成多项式
#define POLYNOMIAL 0x07
// 初始化CRC8查找表
uint8_t crc8_table[256];
void init_crc8_table(void) {
uint8_t i, j;
for (i = 0; i < 256; i++) {
uint8_t crc = i;
for (j = 8; j; j--) {
if (crc & 0x80)
crc = (crc << 1) ^ POLYNOMIAL;
else
crc <<= 1;
}
crc8_table[i] = crc;
}
}
uint8_t crc8(const void *data, size_t len) {
const uint8_t *byte = data;
uint8_t crc = 0x00;
for (; len > 0; len--) {
crc = crc8_table[(crc ^ *byte++) & 0xFF];
}
return crc;
}
int main(int argc, char *argv[]) {
int fd;
uint8_t buffer[4096];
size_t bytes_read;
uint8_t crc;
if (argc != 2) {
fprintf(stderr, "Usage: %s filename\n", argv[0]);
return 1;
}
// 初始化CRC8查找表
init_crc8_table();
// 打开文件
fd = open(argv[1], O_RDONLY);
if (fd == -1) {
perror("Error opening file");
return 1;
}
// 读取文件并计算CRC8校验值
crc = 0x00;
while ((bytes_read = read(fd, buffer, sizeof(buffer))) > 0) {
crc = crc8(buffer, bytes_read);
}
close(fd);
// 输出CRC8校验值
printf("CRC8 checksum: 0x%02X\n", crc);
return 0;
}
这段代码首先定义了一个CRC8查找表,并通过init_crc8_table函数进行初始化。crc8函数用于计算给定数据块的CRC8校验值,它使用查找表来进行快速计算。main函数负责打开文件、读取数据并调用crc8函数来计算整个文件的CRC8校验值。
文件校验-CRC16
下面是使用CRC16并采用CCITT标准生成多项式(0x1021,即多项式x^16 + x^12 + x^5 + x^0)来计算文件CRC16校验值的C语言代码示例。与之前的CRC8示例类似,这里也会使用查找表来优化计算过程。
#include <stdio.h>
#include <stdint.h>
#include <fcntl.h>
#include <unistd.h>
// CRC16 CCITT生成多项式
#define POLYNOMIAL 0x1021
// 初始化CRC16查找表
uint16_t crc16_table[256];
void init_crc16_table(void) {
uint16_t crc, poly;
uint8_t i, j;
for (i = 0; i < 256; i++) {
crc = i;
for (j = 8; j; j--) {
if (crc & 0x0001)
crc = (crc >> 1) ^ POLYNOMIAL;
else
crc >>= 1;
}
crc16_table[i] = crc;
}
}
uint16_t crc16(const void *data, size_t len) {
const uint8_t *byte = data;
uint16_t crc = 0xFFFF;
while (len--) {
crc = (crc >> 8) ^ crc16_table[(crc ^ *byte++) & 0xFF];
}
return crc;
}
int main(int argc, char *argv[]) {
int fd;
uint8_t buffer[4096];
size_t bytes_read;
uint16_t crc;
if (argc != 2) {
fprintf(stderr, "Usage: %s filename\n", argv[0]);
return 1;
}
// 初始化CRC16查找表
init_crc16_table();
// 打开文件
fd = open(argv[1], O_RDONLY);
if (fd == -1) {
perror("Error opening file");
return 1;
}
// 读取文件并计算CRC16校验值
crc = 0xFFFF;
while ((bytes_read = read(fd, buffer, sizeof(buffer))) > 0) {
crc = crc16(buffer, bytes_read);
}
close(fd);
// 输出CRC16校验值
printf("CRC16 checksum: 0x%04X\n", crc);
return 0;
}
这个示例代码中的init_crc16_table函数用于生成CRC16的查找表,而crc16函数则利用该表计算输入数据的CRC16校验值。在主函数main中,程序会读取文件的内容并调用crc16函数计算CRC16校验值,最后输出该值。
文件校验-CRC32
下面是一个使用CRC32算法计算文件校验和的C语言代码示例。这里使用的是IEEE 802.3标准的多项式(0x04C11DB7),这是最常用的CRC32实现。
#include <stdio.h>
#include <stdint.h>
#include <fcntl.h>
#include <unistd.h>
// CRC32 IEEE 802.3生成多项式
#define POLYNOMIAL 0xEDB88320
// 初始化CRC32查找表
uint32_t crc32_table[256];
void init_crc32_table(void) {
uint32_t crc, poly;
uint8_t i, j;
for (i = 0; i < 256; i++) {
crc = i;
for (j = 8; j; j--) {
if (crc & 0x00000001)
crc = (crc >> 1) ^ POLYNOMIAL;
else
crc >>= 1;
}
crc32_table[i] = crc;
}
}
uint32_t crc32(const void *data, size_t len) {
const uint8_t *byte = data;
uint32_t crc = 0xFFFFFFFF;
while (len--){
crc = (crc >> 8) ^ crc32_table[(crc ^ *byte++) & 0xFF];
}
return crc ^ 0xFFFFFFFF;
}
int main(int argc, char *argv[]) {
int fd;
uint8_t buffer[4096];
size_t bytes_read;
uint32_t crc;
if (argc != 2) {
fprintf(stderr, "Usage: %s filename\n", argv[0]);
return 1;
}
// 初始化CRC32查找表
init_crc32_table();
// 打开文件
fd = open(argv[1], O_RDONLY);
if (fd == -1) {
perror("Error opening file");
return 1;
}
// 读取文件并计算CRC32校验值
crc = 0xFFFFFFFF;
while ((bytes_read = read(fd, buffer, sizeof(buffer))) > 0) {
crc = crc32(buffer, bytes_read);
}
close(fd);
// 输出CRC32校验值
printf("CRC32 checksum: 0x%08X\n", crc);
return 0;
}
在这个示例中,init_crc32_table函数初始化了CRC32的查找表,crc32函数用于计算输入数据的CRC32校验值。主函数main负责读取文件内容并调用crc32函数计算CRC32校验值,最后输出该值。
注意,在CRC32计算结束时,通常需要对CRC值进行反转(XOR 0xFFFFFFFF),这是为了与大多数CRC32实现保持一致。
