椭圆曲线数字签名算法ECDSA介绍
Elliptic Curves Cryptography,椭圆曲线密码学(英语:Elliptic curve cryptography,缩写为ECC),一种建立公开密钥加密的算法,基于椭圆曲线数学。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。其主要优势是在某些情况下它比其他的方法使用更小的密钥(比如RSA加密算法)提供相当的或更高等级的安全。ECC的另一个优势是可以定义群之间的双线性映射,基于Weil对或是Tate对;双线性映射已经在密码学中发现了大量的应用,例如基于身份的加密。与传统的基于大质数因子分解困难性的加密方法不同,ECC通过椭圆曲线方程式的性质产生密钥。
ECC 160位的密钥产生一个安全级,相当于RSA 1024位密钥提供的保密强度,而且计算量较小,处理速度更快,存储空间和传输带宽占用较少。目前我国居民二代身份证正在使用 256 位的椭圆曲线密码,虚拟货币比特币也选择ECC作为加密算法。
正式开始前先了解一些基础概念
私钥: 一个秘密数字,只有生成它的人才能知道。其本质上是一个随机生成的数字。
公钥: 与私钥相对应的数字,但不需要保密。可以从私钥中计算出公钥,反之不然。可以使用公共密钥来确定签名是否是真实的(是否为其所发出),而无需泄露私有密钥。
签名: 数字签名是公钥密码的逆应用:用私钥加密消息,用公钥解密消息。用私钥加密的消息称为签名,只有拥有私钥的用户可以生成签名。
证书: 数字证书就是一张附带了数字签名的信息表, 一般包含:公钥,数字签名,公钥拥有者的信息,有效期和发行机构等信息。
更详细的图文介绍可参考David Youd - What is a Digital Signature
对于ECC系统来说,完成运行系统所必须的群操作比同样大小的因数分解系统或模整数离散对数系统要慢。不过,ECC系统的拥护者相信ECDLP问题比DLP或因数分解问题要难的多,并且因此使用ECC能用小的多的密钥长度来提供同等的安全,在这方面来说它确实比例如RSA之类的更快。到目前为止已经公布的结果趋于支持这个结论,不过一些专家表示怀疑。ECC被广泛认为是在给定密钥长度的情况下,最强大的非对称算法,在对带宽要求十分紧张的连接中会十分有用。
优点
安全性高,有研究表示160位的椭圆密钥与1024位的RSA密钥安全性相同。
处理速度快,在私钥的加密解密速度上,ECC算法比RSA、DSA速度更快。
存储空间占用小,因此在网络环境下带宽要求低。
关于ECC,苹果采用的都是NIST标准和规范。但苹果官方API仅为开发者提供了椭圆曲线P-256的256位EC密钥。由于苹果SEP硬件提供的保护机制,私钥会直接以keychain的形式截留在SEP中,不能提取,也不能从外部导入,只能通过引用使用。ECC 是椭圆曲线加密算法(Elliptic curve cryptography)的简称,ECDH 或者 ECDSA是基于它的算法实现。
椭圆曲线数字签名算法(ECDSA)是使用椭圆曲线密码(ECC)对数字签名算法(DSA)的模拟。ECC 是加密算法,无法直接用于数字签名,在 ECC 之前就已经有数字签名(digital signature)技术,如DSA。ECDSA就是使用 ECC 对 DSA 数字签名算法的模拟,最终签名可得到两个值 r 和 s。验证签名只需要求解一个值,判断值是否与 r 相同,如果相同,则说明是有效签名。
技术概要
ECDSA(Elliptic Curve Digital Signature Algorithm),使用椭圆曲线加密算法学进行数字签名的一种算法。安全等级(用bit表示其破解最大可能运算次数),如80bit的公钥,意味着最大可能需要2^80次运算才能找到私钥;在80bit这个安全等级上,ECDSA的公钥长度为160bit,而DSA的公钥长度为320bit,体量上大大缩小。
基本流程
算法的基本思路:
选择一条曲线
选择该曲线上的一个点, 作为你的原点
生成一个随机数, 作为你的私钥
以原点和随机数, 经过一系列神奇的数学运算, 得到你的公钥
生成公钥后, 签名的基本逻辑是:
获取需要签名的数据(或文件)的Hash
使用私钥对该Hash进行签名, 生成R和S详细说明
完成签名后, 其它人验证签名的基本逻辑是:
使用S和公钥, 通过一个神奇的数学运算, 生成R'
对比R和R', 两者相同, 则签名合法. 否则, 非法
简单说明
这个公钥在现在的计算机算力情况下,基本上不可能逆推回私钥,所以在极大程度上是安全的(参考安全等级).而考虑到便利情况下,一般ECDSA的公钥长度会设定为160bit, 即20Byte.
简言之,ECDSA 签名时,已知 Ep(a,b)、基点 G、G 的阶数 n,要经历如下的3步:
1).生成摘要
要签名的内容,实际上并非待签名数据的明文,而是对数据的哈希进行签名。
2).生成签名
3).验证签名(验签)
算法原理简述
1.Hash是数据的摘要结果, 标准的ECDSA使用的是Hash算法是SHA1. 但这个可以进行替换, 如可使用SHA3的算法进行数据摘要. 这个摘要长度越大, 运算量越多, 理论上安全性也越高.
2.椭圆曲线公式y^2 = (x^3 + a * x + b) mod p 和点加法point addition是ECDSA的基础.
3.暗门函数trapdoor function, 要求单向运算简单, 逆向运算困难. ECDSA属于离散对数类的暗门函数的一种, 属于目前理论较成熟, 安全系数相对较高的加密算法.
4.ECDSA算法中需要设置的参数包括: y^2 = (x^3 + a * x + b) mod p 中的 a, b, 指定曲线. p是质数. 还有 N, 椭圆曲线上点的个数, 0 < N < p, 而且N是perfect square. 以及 G, 任意曲线上的点, 作为你运算的原点.
5.只有公钥, 并无法证明私钥签名是否合法, 还需要使用同样的参数进行运算.
DSA [FIPS-186-4] 和 ECDSA [X9.62] 做为两种标准的数字签名方案,它们在各种协议中提供数据完整性和可验证的真实性。它们的一个特点是它们需要为每个签名生成生成一个新的随机值(以下称为k)。为了有效的安全性,必须使用加密安全过程从一组模整数中随机且一致地选择k。在这个过程中即使是轻微的偏斜也可能变成对签名方案的攻击。
对加密安全随机源的需求已被公认是在某些架构中部署 DSA 和 ECDSA 签名方案的障碍,其中安全随机数生成具有挑战性,特别是嵌入式系统,如智能卡。在这些系统中,RSA 签名算法,如公钥密码标准 (PKCS) #1 [RFC3447](使用“类型 1”填充,而不是概率签名方案 (PSS))和 ISO 9796-2 [ISO-9796-2],通常是首选,即使它在计算上更昂贵,因为 RSA(具有此类填充方案)是确定性的,因此不需要随机源。
DSA 和 ECDSA 的随机特性也使得实现更难测试。自动化测试无法可靠地检测实现是否使用了足够高质量的随机源,这使得实施过程更容易受到灾难性故障的影响,通常在系统部署并成功攻击后发现。
通过使用确定性过程生成“随机”值 k,可以将 DSA 和 ECDSA 转化为确定性方案。该过程必须满足一些密码学特征,以保持签名方案所期望的可验证性和不可伪造性; 即对于不知道签名私钥的人,从输入消息到相应 k 值的映射必须在计算上与随机且统一选择的函数(从消息集到可能的 k 值集)将返回的内容没有区别。
部分细节
创建签名:
40字节的签名, 分为2个部分. R和S, 各占20个字节
R的生成:
生成时, 需要先使用随机算法生成一个20字节的k
再使用点乘法运算得到点P, P=k*G
该P点的x坐标值, 则为R
S的生成:
获取数据的Hash值, 计为z
S = k^-1 (z + dA * R) mod p, dA私钥
验证签名:
P = S^-1*z*G + S^-1 * R * Qa, Qa公钥
如果P的x坐标值等于R, 则该签名合法, 否则非法.
算法风险点:
k随机值, 要求为加密强度随机数. 如果其伪随机值可以被猜测/复现, 将意味着被攻击破解. 目前已有的案例为索尼PS3被黑客破解的事件
拓展实现:
secp256k1 Bitcoin实现的Standards for Efficient Cryptography(SEC).这个算法实现是在Bitcoin流行后才被业界逐渐关注和采纳的.其根本原因是比其它实现优化了速度, 提升了约30%.
ECDSA签名机制应用中的安全隐患
如果 k 值泄露, 则任何知道该随机数值的人可以使用该随机数产生签名值恢复私钥
用相同私钥和 k 对两个消息进行签名, 则任何人都可以通过两个签名值恢复出私钥
由于安全的随机数发生器实现的困难性与程序员正确使用随机数的困难性, 业界由随机产生 k 逐渐切换为利用 RFC 6979 中推荐的方式
RFC 6979 中通过利用待签名消息 m 和私钥 d 等信息给出了一种确定性派生 k 的方式
两个用户使用相同的 k 分别对不同的消息进行签名, 则任一方可推算出对方的私钥
由于安全的随机数发生器实现的困难性与程序员正确使用随机数的困难性, 业界由随机产生 k 逐渐切换为利用 RFC 6979 中推荐的方式
RFC 6979 中通过利用待签名消息 m 和私钥 d 等信息给出了一种确定性派生 k 的方式
相同私钥和 k 同时用于 ECDSA 签名和 Schnorr 签名时, 任何人都能够恢复出私钥
ECDSA 签名值的可锻造性
交易 ID 的不唯一会导致根据交易 ID 追踪交 易状态时出现安全隐患.
假设追踪的是携带签名值 σ 的交易的 ID, 而上链的交易中包含的 σ ′ (具有不同的交易的 ID), 则在数字货币交易所处理用户的提币操作时, 当一笔提币已经成功时, 根据交易 ID 进行交易状态跟踪的业务逻辑会认为提币操作失败. 倘若还设置了超时重试机制, 会导致交易所资产的损失。
签名值通常采用的 DER 编码由于编码值并不唯一也会造成区块链网络的分裂
不需要提供签名消息的情况下, 任何人可以根据任意签名值伪造对应私钥的签名值
Craig Wright (澳本聪) 曾经利用此原理通过伪造 Satoshi Nakamoto 的签名值, 进而宣称自己为中本聪
数字签名算法的一些对比
ECDSA 算法是 ECC 算法针对数字签名的变种, 被广泛应用于数字签章和公开金钥加密算法. 比特币所使用的数字签名算法就是 ECDSA.
RSA 算法是 1977 年提出的, 而 ECC 的提出是在 1985 年. 但从数字签名这方面来看, ECDSA 真正流行起来可能还不超过十年. 虽然我没查到 ECDSA 是什么时候诞生的, 但是根据其不支持 Android 4.x 以下和 Windows XP(RSA 可以完全支持), 单就这一点来推断, ECDSA 可能比 1985 要年轻很多. 毕竟 Windows XP 是 01 年的产品, 而安卓 4 也不过才在 11 年底退出.

ECC 证书的历史和好处
RSA当前是公共密钥加密的行业标准,并且在大多数SSL/TLS证书中使用。
椭圆曲线密码术是一种流行的替代方法,它是由两名独立研究人员(Neal Koblitz和Victor S. Miller)于1985年首次提出的,它使用不同的公式化加密方法。尽管RSA基于分解大整数的难度,但ECC依赖于发现随机椭圆曲线的离散对数。换言之,ECC的假设是:虽然可以计算点乘法,但仅给定原始点和乘积点,则几乎不可能计算被乘数。难度随著椭圆曲线的大小而急剧增加。
ECDSA 算法优势
RSA密钥算法是迄今为止的黄金标准,是数字安全中使用最广泛的算法。但是,根据使用移动和紧凑型设备的现代趋势,“纯网络性能”是整个业务的重中之重。从这个角度来看,密钥的物理大小是一个主要问题。
ECDSA 的公钥私钥长度更短,加密后的信息也会更小,因此计算处理花费的时间会更短,并且内存和带宽的需求也会更小。
较小的ECC密钥具有与较大的RSA密钥相当的强度,这是因为生成密钥的算法不同。例如,256位ECC密钥等效于3072位RSA密钥,而384位ECC密钥等效于7680位RSA密钥。
安全强度(位) RSA公钥长度(位) ECDSA公钥长度(位)
80 1024 160
112 2048 224
128 3072 256
192 7680 384
256 15360 512
DSA和RSA密钥算法需要较大的密钥大小,并且可能因分解大量数字而失败。 对于ECDSA,需要解决椭圆曲线离散对数问题(ECDLP)才能破解密钥,到目前为止,尚未实现任何重大进展。 因此,ECC证书提供了更好的安全解决方案,并且使用普通黑客的“蛮力”方法更难以破解。
ECDSA 的劣势
验证签名上 RSA 似乎比 ECDSA 快得多,参见SSL.com - Comparing ECDSA vs RSA
但是应该只有在第一次连接域名的时候才会验证证书,可以大概认为每次上网的时候 ECC 会多一小段的延迟;但是除了证书的验证之外,其他方面(加密解密运算, 带宽占用)不会受影响。
ECDSA 算法的后量子抗性
ECDSA 算法的担忧主要在于量子抗性不足,前文讲到一般的黑客在面对 ECDSA 算法时,使用穷举法一定是会碰壁的;但是如果攻击者拥有大型量子计算机,那么他可以使用秀尔算法解决离散对数问题,从而破解私钥和共享秘密。这是该算法目前面对的一个难题。
美国国家标准技术研究院(NIST)已在其Suite B(套件B是一种已有20年历史的公共加密标准)推荐算法集中认可了椭圆曲线密码学,特别是用于密钥交换的椭圆曲线Diffie-Hellman(ECDH)和用于数字签名的椭圆曲线数字签名算法(ECDSA)。美国国家安全局(NSA)允许其用于保护通过384位密钥分类为最高机密的信息。但是,由于担心对ECC进行量子计算攻击,美国国家安全局(NSA)于2015年8月宣布,计划用新的密码套件替换套件B。
目前的估算认为:破解256位素数域上的椭圆曲线,需要2330个量子比特与1260亿个托佛利门。相比之下,使用秀尔算法破解2048位的RSA则需要4098个量子比特与5.2万亿个托佛利门。因此,椭圆曲线会更先遭到量子计算机的破解。但目前还不存在建造如此大型量子计算机的科学技术,因此椭圆曲线密码学至少在未来十年(或更久)依然是安全的。
ECDSA 的兼容性
只要你的设备不太旧, 通常都能支持 ECDSA. 以下是关于 ECDSA 所需的浏览器, 操作系统, 服务器框架的最低版本要求.
浏览器 所需的最低版本
Firefox 2.0
Chrome 1.0
IE 7
Safari 4
操作系统 所需的最低版本
Windows Vista
MacOS OS X 10.6
Android 4.0
Red Hat Enterprise Linux 6.5
服务器框架 所需的最低版本
Apache HTTP Server 2.2.26
Nginx 1.1.0
Windows Server 2008
Apache Tomcat 1.1.30
Dovecot 2.2.5
IBM HTTP Server 8.0 w/ PM80235
Sun Java System Web Server 7.0
关于secp256k1
它是高效密码组标准(SECG) 协会开发的一套高效的椭圆曲线签名算法标准。在比特币流行之前,secp256k1 并未真正使用过。自从比特币之后,secp2256k1 已成为数字货币中默认的数字签名算法。大多数常用的曲线具有一个随机的结构,但是 secp256k1 是为了更有效率的计算而构造了一个非随机结构。因此如果该算法的实现通过合理的优化,其计算效率可以比别的曲线快 30% 以上。同时与常用的 NIST 曲线不同,secp256k1 的常量是通过可预测的方式挑选的,这可以有效的减少防止曲线设计者安置后门的可能性,secp256k1 是一条基于有限域的 Koblitz 椭圆曲线。
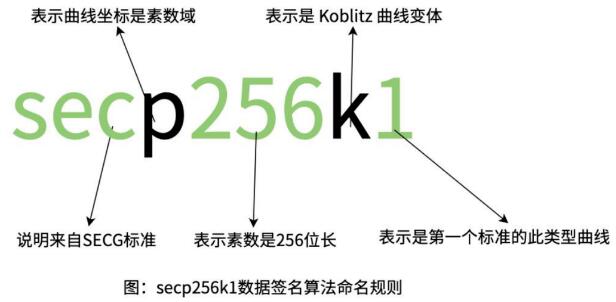
为什么比特币要选择 secp256k1 签名算法而不是其他算法呢?比特币开发者社区曾讨论过 secp256k1 是否安全。中本聪没有明确解释,只是说道“有根据的推测”。
社区的讨论不外乎是在安全和效率上做权衡,选择一个不受任何政府控制、无后门的签名算法是比特币的首要考虑因素;其次也需要提供计算速度,毕竟在比特币中签名与验签是不断在处理的事情(60%左右的 CPU 时间几乎全用在这上面),而具有可预测性、高计算效率特性的 Koblitz 曲线是不错的选择。除椭圆曲线签名算法使用非常短的私钥和签名值外。基于安全第一,效率第二原则,secp256k1 就是一个优解,以太坊的签名算法也是采用 secp256k1。
EC家族一览
ECDSA is a digital signature algorithm
ECIES is an Integrated Encryption scheme
ECDH is a key secure key exchange algorithm
Digital signature algorithms are used to authenticate a digital content. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, such that the sender cannot deny having sent the message (authentication and non-repudiation) and that the message was not altered in transit (integrity).
Integrated Encryption scheme is a hybrid encryption scheme which provides semantic security against chosen plain text and chosen cipher text attacks. ECIES uses different types of functions:
Key Agreement function
Key Derivation Function
Symmetric Encryption scheme
Hash function
Secure key exchange algorithms are used to exchange our keys securely via a non secure channel.
Here you are interested in Elliptic Curve variants of those algorithms. Your requirement is to exchange some data. So you can use ECDH to share the secret key and ECDSA to sign the content. Because ECDH does not provide authentication we can use ECDSA for that purpose. Once the secret key is shared, you can securely exchange your data through a non secure channel. Strength of the secret key can be defined by considering the level of security you need and amount of computation power you got.
ECC
上文有述。ECC的参数有很多,通过openssl ecparam -list_curves查看。
ECDH
椭圆曲线迪菲-赫尔曼金钥交换(英语:Elliptic Curve Diffie–Hellman key Exchange,缩写为ECDH),一种匿名的密钥合意协议(Key-agreement protocol)。在这个协定下,双方通过Diffie–Hellman密钥交换算法,利用由椭圆曲线加密建立的公钥与私钥对,在一个不安全的通道中,建立起安全的共有加密资料。这是迪菲-赫尔曼密钥交换的变种,采用椭圆曲线加密来加强安全性。
ECDH主要是用来在一个不安全的通道中建立起安全的共有加密资料,一般来说交换的都是私钥,这个密钥一般作为“对称加密”的密钥而被双方在后续数据传输中使用。ECDH是ECC算法和DH结合使用,用于密钥磋商,这个密钥交换算法称为ECDH。交换双方可以在不共享任何秘密的情况下协商出一个密钥。ECC是建立在基于椭圆曲线的离散对数问题上的密码体制。
是基于ECC(Elliptic Curve Cryptosystems,椭圆曲线密码体制,参看ECC)的DH( Diffie-Hellman)密钥交换算法。
用途:由于通过ECDH,双方可以在不共享任何秘密的前提下协商出一个共享秘密,因此ECDH广泛用于协议之中,通过ECDH得到对称加密密钥。如TLS中的*_ECDH_*密码套件。使用DH算法的协议,都可以升级到ECDH算法。ECDH具有ECC的高强度、短密钥长度、计算速度快等优点。
密钥交换过程:假设密钥交换双方为Alice、Bob,其有共享曲线参数(椭圆曲线E、阶N、基点G):
1.Alice生成随机整数a,计算A=a*G。Bob生成随机整数b,计算B=b*G。
2.Alice将A传递给Bob。A的传递可以公开,即攻击者可以获取A。由于椭圆曲线的离散对数问题是难题,所以攻击者不可以通过A、G计算出a。Bob将B传递给Alice。同理,B的传递可以公开。
3.Bob收到Alice传递的A,计算Q=b*A
4.Alice收到Bob传递的B,计算Q‘=a*B
小结:Alice、Bob双方即得Q=b*A=b*(a*G)=(b*a)*G=(a*b)*G=a*(b*G)=a*B=Q' (交换律和结合律),即双方得到一致的密钥Q。
ECDSA
ECDSA(椭圆曲线数字签名算法)是DSA(数字签名算法)的椭圆曲线实现。椭圆曲线密码术能够以较小的密钥提供与RSA相对相同的安全级别。它还具有DSA对不良RNG敏感的缺点。
ECDSA是数字签名算法,是DSA的变体。在数字签名算法中,消息发送方对消息进行签名,消息接收方对消息验签,这样能够保证数据的完整性(保证消息内容未被第三方篡改)、消息源鉴别(确定消息是由本人发出,而不是他人伪造)和不可否认性(消息发送方无法否认自己发出过这则消息)。
用于数字签名,是ECC与DSA的结合,整个签名过程与DSA类似,所不一样的是签名中采取的算法为ECC,最后签名出来的值也是分为r,s。
参考来源:
ExDSA
开始使用 ECC 证书
大白话椭圆曲线加密算法
ECDSA和DSA的确定性用法
区块链中的ECDSA的安全性
ECDSA算法如何保护你的数据(上)
ECDSA算法如何保护你的数据(下)
ECC 160位的密钥产生一个安全级,相当于RSA 1024位密钥提供的保密强度,而且计算量较小,处理速度更快,存储空间和传输带宽占用较少。目前我国居民二代身份证正在使用 256 位的椭圆曲线密码,虚拟货币比特币也选择ECC作为加密算法。
正式开始前先了解一些基础概念
私钥: 一个秘密数字,只有生成它的人才能知道。其本质上是一个随机生成的数字。
公钥: 与私钥相对应的数字,但不需要保密。可以从私钥中计算出公钥,反之不然。可以使用公共密钥来确定签名是否是真实的(是否为其所发出),而无需泄露私有密钥。
签名: 数字签名是公钥密码的逆应用:用私钥加密消息,用公钥解密消息。用私钥加密的消息称为签名,只有拥有私钥的用户可以生成签名。
证书: 数字证书就是一张附带了数字签名的信息表, 一般包含:公钥,数字签名,公钥拥有者的信息,有效期和发行机构等信息。
更详细的图文介绍可参考David Youd - What is a Digital Signature
对于ECC系统来说,完成运行系统所必须的群操作比同样大小的因数分解系统或模整数离散对数系统要慢。不过,ECC系统的拥护者相信ECDLP问题比DLP或因数分解问题要难的多,并且因此使用ECC能用小的多的密钥长度来提供同等的安全,在这方面来说它确实比例如RSA之类的更快。到目前为止已经公布的结果趋于支持这个结论,不过一些专家表示怀疑。ECC被广泛认为是在给定密钥长度的情况下,最强大的非对称算法,在对带宽要求十分紧张的连接中会十分有用。
优点
安全性高,有研究表示160位的椭圆密钥与1024位的RSA密钥安全性相同。
处理速度快,在私钥的加密解密速度上,ECC算法比RSA、DSA速度更快。
存储空间占用小,因此在网络环境下带宽要求低。
关于ECC,苹果采用的都是NIST标准和规范。但苹果官方API仅为开发者提供了椭圆曲线P-256的256位EC密钥。由于苹果SEP硬件提供的保护机制,私钥会直接以keychain的形式截留在SEP中,不能提取,也不能从外部导入,只能通过引用使用。ECC 是椭圆曲线加密算法(Elliptic curve cryptography)的简称,ECDH 或者 ECDSA是基于它的算法实现。
椭圆曲线数字签名算法(ECDSA)是使用椭圆曲线密码(ECC)对数字签名算法(DSA)的模拟。ECC 是加密算法,无法直接用于数字签名,在 ECC 之前就已经有数字签名(digital signature)技术,如DSA。ECDSA就是使用 ECC 对 DSA 数字签名算法的模拟,最终签名可得到两个值 r 和 s。验证签名只需要求解一个值,判断值是否与 r 相同,如果相同,则说明是有效签名。
技术概要
ECDSA(Elliptic Curve Digital Signature Algorithm),使用椭圆曲线加密算法学进行数字签名的一种算法。安全等级(用bit表示其破解最大可能运算次数),如80bit的公钥,意味着最大可能需要2^80次运算才能找到私钥;在80bit这个安全等级上,ECDSA的公钥长度为160bit,而DSA的公钥长度为320bit,体量上大大缩小。
基本流程
算法的基本思路:
选择一条曲线
选择该曲线上的一个点, 作为你的原点
生成一个随机数, 作为你的私钥
以原点和随机数, 经过一系列神奇的数学运算, 得到你的公钥
生成公钥后, 签名的基本逻辑是:
获取需要签名的数据(或文件)的Hash
使用私钥对该Hash进行签名, 生成R和S详细说明
完成签名后, 其它人验证签名的基本逻辑是:
使用S和公钥, 通过一个神奇的数学运算, 生成R'
对比R和R', 两者相同, 则签名合法. 否则, 非法
简单说明
这个公钥在现在的计算机算力情况下,基本上不可能逆推回私钥,所以在极大程度上是安全的(参考安全等级).而考虑到便利情况下,一般ECDSA的公钥长度会设定为160bit, 即20Byte.
简言之,ECDSA 签名时,已知 Ep(a,b)、基点 G、G 的阶数 n,要经历如下的3步:
1).生成摘要
要签名的内容,实际上并非待签名数据的明文,而是对数据的哈希进行签名。
2).生成签名
3).验证签名(验签)
算法原理简述
1.Hash是数据的摘要结果, 标准的ECDSA使用的是Hash算法是SHA1. 但这个可以进行替换, 如可使用SHA3的算法进行数据摘要. 这个摘要长度越大, 运算量越多, 理论上安全性也越高.
2.椭圆曲线公式y^2 = (x^3 + a * x + b) mod p 和点加法point addition是ECDSA的基础.
3.暗门函数trapdoor function, 要求单向运算简单, 逆向运算困难. ECDSA属于离散对数类的暗门函数的一种, 属于目前理论较成熟, 安全系数相对较高的加密算法.
4.ECDSA算法中需要设置的参数包括: y^2 = (x^3 + a * x + b) mod p 中的 a, b, 指定曲线. p是质数. 还有 N, 椭圆曲线上点的个数, 0 < N < p, 而且N是perfect square. 以及 G, 任意曲线上的点, 作为你运算的原点.
5.只有公钥, 并无法证明私钥签名是否合法, 还需要使用同样的参数进行运算.
DSA [FIPS-186-4] 和 ECDSA [X9.62] 做为两种标准的数字签名方案,它们在各种协议中提供数据完整性和可验证的真实性。它们的一个特点是它们需要为每个签名生成生成一个新的随机值(以下称为k)。为了有效的安全性,必须使用加密安全过程从一组模整数中随机且一致地选择k。在这个过程中即使是轻微的偏斜也可能变成对签名方案的攻击。
对加密安全随机源的需求已被公认是在某些架构中部署 DSA 和 ECDSA 签名方案的障碍,其中安全随机数生成具有挑战性,特别是嵌入式系统,如智能卡。在这些系统中,RSA 签名算法,如公钥密码标准 (PKCS) #1 [RFC3447](使用“类型 1”填充,而不是概率签名方案 (PSS))和 ISO 9796-2 [ISO-9796-2],通常是首选,即使它在计算上更昂贵,因为 RSA(具有此类填充方案)是确定性的,因此不需要随机源。
DSA 和 ECDSA 的随机特性也使得实现更难测试。自动化测试无法可靠地检测实现是否使用了足够高质量的随机源,这使得实施过程更容易受到灾难性故障的影响,通常在系统部署并成功攻击后发现。
通过使用确定性过程生成“随机”值 k,可以将 DSA 和 ECDSA 转化为确定性方案。该过程必须满足一些密码学特征,以保持签名方案所期望的可验证性和不可伪造性; 即对于不知道签名私钥的人,从输入消息到相应 k 值的映射必须在计算上与随机且统一选择的函数(从消息集到可能的 k 值集)将返回的内容没有区别。
部分细节
创建签名:
40字节的签名, 分为2个部分. R和S, 各占20个字节
R的生成:
生成时, 需要先使用随机算法生成一个20字节的k
再使用点乘法运算得到点P, P=k*G
该P点的x坐标值, 则为R
S的生成:
获取数据的Hash值, 计为z
S = k^-1 (z + dA * R) mod p, dA私钥
验证签名:
P = S^-1*z*G + S^-1 * R * Qa, Qa公钥
如果P的x坐标值等于R, 则该签名合法, 否则非法.
算法风险点:
k随机值, 要求为加密强度随机数. 如果其伪随机值可以被猜测/复现, 将意味着被攻击破解. 目前已有的案例为索尼PS3被黑客破解的事件
拓展实现:
secp256k1 Bitcoin实现的Standards for Efficient Cryptography(SEC).这个算法实现是在Bitcoin流行后才被业界逐渐关注和采纳的.其根本原因是比其它实现优化了速度, 提升了约30%.
ECDSA签名机制应用中的安全隐患
如果 k 值泄露, 则任何知道该随机数值的人可以使用该随机数产生签名值恢复私钥
用相同私钥和 k 对两个消息进行签名, 则任何人都可以通过两个签名值恢复出私钥
由于安全的随机数发生器实现的困难性与程序员正确使用随机数的困难性, 业界由随机产生 k 逐渐切换为利用 RFC 6979 中推荐的方式
RFC 6979 中通过利用待签名消息 m 和私钥 d 等信息给出了一种确定性派生 k 的方式
两个用户使用相同的 k 分别对不同的消息进行签名, 则任一方可推算出对方的私钥
由于安全的随机数发生器实现的困难性与程序员正确使用随机数的困难性, 业界由随机产生 k 逐渐切换为利用 RFC 6979 中推荐的方式
RFC 6979 中通过利用待签名消息 m 和私钥 d 等信息给出了一种确定性派生 k 的方式
相同私钥和 k 同时用于 ECDSA 签名和 Schnorr 签名时, 任何人都能够恢复出私钥
ECDSA 签名值的可锻造性
交易 ID 的不唯一会导致根据交易 ID 追踪交 易状态时出现安全隐患.
假设追踪的是携带签名值 σ 的交易的 ID, 而上链的交易中包含的 σ ′ (具有不同的交易的 ID), 则在数字货币交易所处理用户的提币操作时, 当一笔提币已经成功时, 根据交易 ID 进行交易状态跟踪的业务逻辑会认为提币操作失败. 倘若还设置了超时重试机制, 会导致交易所资产的损失。
签名值通常采用的 DER 编码由于编码值并不唯一也会造成区块链网络的分裂
不需要提供签名消息的情况下, 任何人可以根据任意签名值伪造对应私钥的签名值
Craig Wright (澳本聪) 曾经利用此原理通过伪造 Satoshi Nakamoto 的签名值, 进而宣称自己为中本聪
数字签名算法的一些对比
ECDSA 算法是 ECC 算法针对数字签名的变种, 被广泛应用于数字签章和公开金钥加密算法. 比特币所使用的数字签名算法就是 ECDSA.
RSA 算法是 1977 年提出的, 而 ECC 的提出是在 1985 年. 但从数字签名这方面来看, ECDSA 真正流行起来可能还不超过十年. 虽然我没查到 ECDSA 是什么时候诞生的, 但是根据其不支持 Android 4.x 以下和 Windows XP(RSA 可以完全支持), 单就这一点来推断, ECDSA 可能比 1985 要年轻很多. 毕竟 Windows XP 是 01 年的产品, 而安卓 4 也不过才在 11 年底退出.

ECC 证书的历史和好处
RSA当前是公共密钥加密的行业标准,并且在大多数SSL/TLS证书中使用。
椭圆曲线密码术是一种流行的替代方法,它是由两名独立研究人员(Neal Koblitz和Victor S. Miller)于1985年首次提出的,它使用不同的公式化加密方法。尽管RSA基于分解大整数的难度,但ECC依赖于发现随机椭圆曲线的离散对数。换言之,ECC的假设是:虽然可以计算点乘法,但仅给定原始点和乘积点,则几乎不可能计算被乘数。难度随著椭圆曲线的大小而急剧增加。
ECDSA 算法优势
RSA密钥算法是迄今为止的黄金标准,是数字安全中使用最广泛的算法。但是,根据使用移动和紧凑型设备的现代趋势,“纯网络性能”是整个业务的重中之重。从这个角度来看,密钥的物理大小是一个主要问题。
ECDSA 的公钥私钥长度更短,加密后的信息也会更小,因此计算处理花费的时间会更短,并且内存和带宽的需求也会更小。
较小的ECC密钥具有与较大的RSA密钥相当的强度,这是因为生成密钥的算法不同。例如,256位ECC密钥等效于3072位RSA密钥,而384位ECC密钥等效于7680位RSA密钥。
安全强度(位) RSA公钥长度(位) ECDSA公钥长度(位)
80 1024 160
112 2048 224
128 3072 256
192 7680 384
256 15360 512
DSA和RSA密钥算法需要较大的密钥大小,并且可能因分解大量数字而失败。 对于ECDSA,需要解决椭圆曲线离散对数问题(ECDLP)才能破解密钥,到目前为止,尚未实现任何重大进展。 因此,ECC证书提供了更好的安全解决方案,并且使用普通黑客的“蛮力”方法更难以破解。
ECDSA 的劣势
验证签名上 RSA 似乎比 ECDSA 快得多,参见SSL.com - Comparing ECDSA vs RSA
但是应该只有在第一次连接域名的时候才会验证证书,可以大概认为每次上网的时候 ECC 会多一小段的延迟;但是除了证书的验证之外,其他方面(加密解密运算, 带宽占用)不会受影响。
ECDSA 算法的后量子抗性
ECDSA 算法的担忧主要在于量子抗性不足,前文讲到一般的黑客在面对 ECDSA 算法时,使用穷举法一定是会碰壁的;但是如果攻击者拥有大型量子计算机,那么他可以使用秀尔算法解决离散对数问题,从而破解私钥和共享秘密。这是该算法目前面对的一个难题。
美国国家标准技术研究院(NIST)已在其Suite B(套件B是一种已有20年历史的公共加密标准)推荐算法集中认可了椭圆曲线密码学,特别是用于密钥交换的椭圆曲线Diffie-Hellman(ECDH)和用于数字签名的椭圆曲线数字签名算法(ECDSA)。美国国家安全局(NSA)允许其用于保护通过384位密钥分类为最高机密的信息。但是,由于担心对ECC进行量子计算攻击,美国国家安全局(NSA)于2015年8月宣布,计划用新的密码套件替换套件B。
目前的估算认为:破解256位素数域上的椭圆曲线,需要2330个量子比特与1260亿个托佛利门。相比之下,使用秀尔算法破解2048位的RSA则需要4098个量子比特与5.2万亿个托佛利门。因此,椭圆曲线会更先遭到量子计算机的破解。但目前还不存在建造如此大型量子计算机的科学技术,因此椭圆曲线密码学至少在未来十年(或更久)依然是安全的。
ECDSA 的兼容性
只要你的设备不太旧, 通常都能支持 ECDSA. 以下是关于 ECDSA 所需的浏览器, 操作系统, 服务器框架的最低版本要求.
浏览器 所需的最低版本
Firefox 2.0
Chrome 1.0
IE 7
Safari 4
操作系统 所需的最低版本
Windows Vista
MacOS OS X 10.6
Android 4.0
Red Hat Enterprise Linux 6.5
服务器框架 所需的最低版本
Apache HTTP Server 2.2.26
Nginx 1.1.0
Windows Server 2008
Apache Tomcat 1.1.30
Dovecot 2.2.5
IBM HTTP Server 8.0 w/ PM80235
Sun Java System Web Server 7.0
关于secp256k1
它是高效密码组标准(SECG) 协会开发的一套高效的椭圆曲线签名算法标准。在比特币流行之前,secp256k1 并未真正使用过。自从比特币之后,secp2256k1 已成为数字货币中默认的数字签名算法。大多数常用的曲线具有一个随机的结构,但是 secp256k1 是为了更有效率的计算而构造了一个非随机结构。因此如果该算法的实现通过合理的优化,其计算效率可以比别的曲线快 30% 以上。同时与常用的 NIST 曲线不同,secp256k1 的常量是通过可预测的方式挑选的,这可以有效的减少防止曲线设计者安置后门的可能性,secp256k1 是一条基于有限域的 Koblitz 椭圆曲线。

为什么比特币要选择 secp256k1 签名算法而不是其他算法呢?比特币开发者社区曾讨论过 secp256k1 是否安全。中本聪没有明确解释,只是说道“有根据的推测”。
社区的讨论不外乎是在安全和效率上做权衡,选择一个不受任何政府控制、无后门的签名算法是比特币的首要考虑因素;其次也需要提供计算速度,毕竟在比特币中签名与验签是不断在处理的事情(60%左右的 CPU 时间几乎全用在这上面),而具有可预测性、高计算效率特性的 Koblitz 曲线是不错的选择。除椭圆曲线签名算法使用非常短的私钥和签名值外。基于安全第一,效率第二原则,secp256k1 就是一个优解,以太坊的签名算法也是采用 secp256k1。
EC家族一览
ECDSA is a digital signature algorithm
ECIES is an Integrated Encryption scheme
ECDH is a key secure key exchange algorithm
Digital signature algorithms are used to authenticate a digital content. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, such that the sender cannot deny having sent the message (authentication and non-repudiation) and that the message was not altered in transit (integrity).
Integrated Encryption scheme is a hybrid encryption scheme which provides semantic security against chosen plain text and chosen cipher text attacks. ECIES uses different types of functions:
Key Agreement function
Key Derivation Function
Symmetric Encryption scheme
Hash function
Secure key exchange algorithms are used to exchange our keys securely via a non secure channel.
Here you are interested in Elliptic Curve variants of those algorithms. Your requirement is to exchange some data. So you can use ECDH to share the secret key and ECDSA to sign the content. Because ECDH does not provide authentication we can use ECDSA for that purpose. Once the secret key is shared, you can securely exchange your data through a non secure channel. Strength of the secret key can be defined by considering the level of security you need and amount of computation power you got.
ECC
上文有述。ECC的参数有很多,通过openssl ecparam -list_curves查看。
ECDH
椭圆曲线迪菲-赫尔曼金钥交换(英语:Elliptic Curve Diffie–Hellman key Exchange,缩写为ECDH),一种匿名的密钥合意协议(Key-agreement protocol)。在这个协定下,双方通过Diffie–Hellman密钥交换算法,利用由椭圆曲线加密建立的公钥与私钥对,在一个不安全的通道中,建立起安全的共有加密资料。这是迪菲-赫尔曼密钥交换的变种,采用椭圆曲线加密来加强安全性。
ECDH主要是用来在一个不安全的通道中建立起安全的共有加密资料,一般来说交换的都是私钥,这个密钥一般作为“对称加密”的密钥而被双方在后续数据传输中使用。ECDH是ECC算法和DH结合使用,用于密钥磋商,这个密钥交换算法称为ECDH。交换双方可以在不共享任何秘密的情况下协商出一个密钥。ECC是建立在基于椭圆曲线的离散对数问题上的密码体制。
是基于ECC(Elliptic Curve Cryptosystems,椭圆曲线密码体制,参看ECC)的DH( Diffie-Hellman)密钥交换算法。
用途:由于通过ECDH,双方可以在不共享任何秘密的前提下协商出一个共享秘密,因此ECDH广泛用于协议之中,通过ECDH得到对称加密密钥。如TLS中的*_ECDH_*密码套件。使用DH算法的协议,都可以升级到ECDH算法。ECDH具有ECC的高强度、短密钥长度、计算速度快等优点。
密钥交换过程:假设密钥交换双方为Alice、Bob,其有共享曲线参数(椭圆曲线E、阶N、基点G):
1.Alice生成随机整数a,计算A=a*G。Bob生成随机整数b,计算B=b*G。
2.Alice将A传递给Bob。A的传递可以公开,即攻击者可以获取A。由于椭圆曲线的离散对数问题是难题,所以攻击者不可以通过A、G计算出a。Bob将B传递给Alice。同理,B的传递可以公开。
3.Bob收到Alice传递的A,计算Q=b*A
4.Alice收到Bob传递的B,计算Q‘=a*B
小结:Alice、Bob双方即得Q=b*A=b*(a*G)=(b*a)*G=(a*b)*G=a*(b*G)=a*B=Q' (交换律和结合律),即双方得到一致的密钥Q。
ECDSA
ECDSA(椭圆曲线数字签名算法)是DSA(数字签名算法)的椭圆曲线实现。椭圆曲线密码术能够以较小的密钥提供与RSA相对相同的安全级别。它还具有DSA对不良RNG敏感的缺点。
ECDSA是数字签名算法,是DSA的变体。在数字签名算法中,消息发送方对消息进行签名,消息接收方对消息验签,这样能够保证数据的完整性(保证消息内容未被第三方篡改)、消息源鉴别(确定消息是由本人发出,而不是他人伪造)和不可否认性(消息发送方无法否认自己发出过这则消息)。
用于数字签名,是ECC与DSA的结合,整个签名过程与DSA类似,所不一样的是签名中采取的算法为ECC,最后签名出来的值也是分为r,s。
参考来源:
ExDSA
开始使用 ECC 证书
大白话椭圆曲线加密算法
ECDSA和DSA的确定性用法
区块链中的ECDSA的安全性
ECDSA算法如何保护你的数据(上)
ECDSA算法如何保护你的数据(下)
