加解密算法之对称密钥加密
对称密钥算法(英语:Symmetric-key algorithm)又称为对称加密、私钥加密、共享密钥加密,是密码学中的一类加密算法。这类算法在加密和解密时使用相同的密钥,或是使用两个可以简单地相互推算的密钥。所谓对称加密算法,说得直白一点,就是加密与解密的过程一模一样。事实上,这组密钥成为在两个或多个成员间的共同秘密,以便维持专属的通信联系。与公开密钥加密相比,要求双方获取相同的密钥是对称密钥加密的主要缺点之一。本文可以认为是《理解分组密码》的升级加强版,部分内容摘自于钱魏Way的个人博客,感谢。
网络安全通信中要用到两类密码算法,一类是对称密码算法,另一类是非对称密码算法。对称密码算法的加密密钥能够从解密密钥中推算出来,反过来也成立。在大多数对称算法中,加密解密密钥是相同的。它要求发送者和接收者在安全通信之前,商定一个密钥。对称算法的安全性依赖于密钥,泄漏密钥就意味着任何人都能对消息进行加密解密。只要通信需要保密,密钥就必须保密。
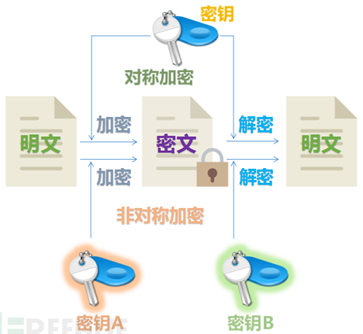
对称算法又可分为两类。一次只对明文中的单个位(有时对字节)运算的算法称为序列算法或序列密码。另一类算法是对明文的一组位进行运算,这些位组称为分组,相应的算法称为分组算法或分组密码。现代计算机密码算法的典型分组长度为64位――这个长度既考虑到分析破译密码的难度,又考虑到使用的方便性。后来,随着破译能力的发展,分组长度又提高到128位或更长。
常用的采用对称密码术的加密方案有5个组成部分:
明文:原始信息。
加密算法:以密钥为参数,对明文进行多种置换和转换的规则和步骤,变换结果为密文。
密钥:加密与解密算法的参数,直接影响对明文进行变换的结果。
密文:对明文进行变换的结果。
解密算法:加密算法的逆变换,以密文为输入、密钥为参数,变换结果为明文。
对称密码当中有几种常用到的数学运算。这些运算的共同目的就是把被加密的明文数码尽可能深地打乱,从而加大破译的难度。
移位和循环移位:移位就是将一段数码按照规定的位数整体性地左移或右移。循环右移就是当右移时,把数码的最后的位移到数码的最前头,循环左移正相反。例如对十进制数码12345678循环右移1位(十进制位)的结果为81234567,而循环左移1位的结果则为23456781。
置换:就是将数码中的某一位的值根据置换表的规定,用另一位代替。它不像移位操作那样整齐有序,看上去杂乱无章。这正是加密所需,被经常应用。
扩展:就是将一段数码扩展成比原来位数更长的数码。扩展方法有多种,例如,可以用置换的方法,以扩展置换表来规定扩展后的数码每一位的替代值。
压缩:就是将一段数码压缩成比原来位数更短的数码。压缩方法有多种,例如,也可以用置换的方法,以表来规定压缩后的数码每一位的替代值。
异或:这是一种二进制布尔代数运算。也可以简单地理解为,参与异或运算的两数位如相等,则结果为0,不等则为1。异或的数学符号为⊕。
迭代:迭代就是多次重复相同的运算,这在密码算法中经常使用,以使得形成的密文更加难以破解。
常见的对称加密算法有AES、ChaCha20、3DES、Salsa20、DES、Blowfish、IDEA、RC5、RC6、Camellia。对称加密的速度比公钥加密快很多,在很多场合都需要对称加密。
RC4
假设定义RC4的运算过程是rc4(key,data),那么密文=rc4(key,明文),明文=rc4(key,密文)。所以对一段数据迭代地做奇数次RC4运算,就得到密文,对这段数据迭代地做偶数次RC4运算,结果依旧是原来的那段数据。
这种对称性就是基于密钥流的加密算法的一个特征。RC4加密算法也是一种基于密钥流的加密算法。何为密钥流呢?假设要加密的数据长N个字节,那么我通过某种算法,也产生一串N字节的数据,然后把这两串N字节数据按位异或(XOR),就得到了密文。把密文与这串密钥流再XOR,就能重新得到明文。而这一串由某种算法产生的N字节,或者说8N位,就叫做密钥流,而该算法就叫做密钥流生成算法。所有基于密钥流的加密算法的区别就在于密钥流的生成方式的不同。只要生成了与数据等长的密钥流,那么加密、解密方式都是把数据与密钥流做异或运算。
RC4本质上就是一种密钥流生成算法。它的特点是算法简单、运算效率高,而且非线性度良好。算法简单的特点使得可以使用硬件来实现RC4,如同在很多旧的无线网卡中就是使用硬件来实现WEP加密的。运算效率高使得用软件实现RC4也很便捷、不会占用过多CPU。而非线性度良好,则是RC4广泛使用的重要原因。所谓非线性度好,就是指通过密码产生密钥流容易,而通过密钥流逆推出密码则很难。
RC4 算法的特点是算法简单,运行速度快,而且密钥长度是可变的,密钥长度范围为 1-256 字节。
算法原理
RC4算法主要包括两个部分:1)使用 key-scheduling algorithm (KSA) 算法根据用户输入的秘钥 key 生成 S 盒;2)使用 Pseudo-random generation algorithm (PRGA) 算法生成秘钥流用于加密数据。
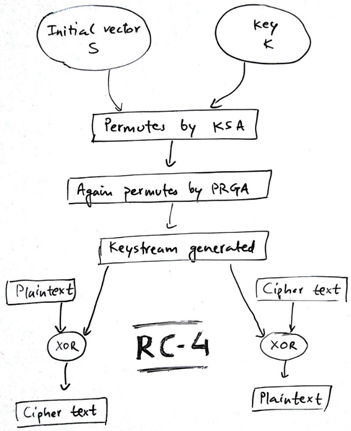
利用Key生成S盒——The key-scheduling algorithm (KSA)
KSA算法初始化长度为 256 的 S 盒。第一个 for 循环将 0 到 255 的互不重复的元素装入 S 盒;第二个 for 循环根据密钥打乱 S 盒。
for i from 0 to 255
S[i] := i
endfor
j := 0
for i from 0 to 255
j := (j + S[i] + key[i mod keylength]) mod 256
swap values of S[i] and S[j]
endfor
利用S盒生成密钥流——The pseudo-random generation algorithm(PRGA)
Pseudo-random generation algorithm (PRGA) 算法根据 S 盒生成与明文长度相同的秘钥流,使用秘钥流加密明文。秘钥流的生成如下图所示:
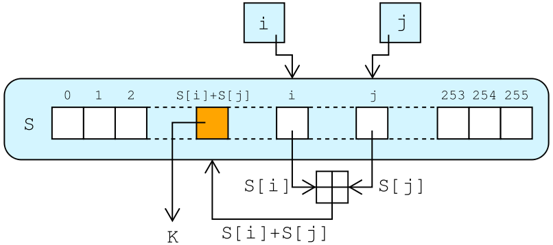
循环体中每收到一个字节,a 和 b 定位S盒中的一个元素,并与输入字节异或,得到密文 k;同时,c 还改变了 S 盒。由于异或运算的特性,使得加密与解密过程一致。如果输入的是明文,输出的就是密文;如果输入的是密文,输出的就是明文。
i := 0
j := 0
while GeneratingOutput:
i := (i + 1) mod 256 // a
j := (j + S[i]) mod 256 // b
swap values of S[i] and S[j] // c
K := inputByte ^ S[(S[i] + S[j]) mod 256] // d
output K
endwhile
DES
美国国家标准局1973年开始研究除国防部外的其它部门的计算机系统的数据加密标准,于1973年5月15日和1974年8月27日先后两次向公众发出了征求加密算法的公告。加密算法要达到的目的(通常称为DES 密码算法要求)主要为以下四点:
提供高质量的数据保护,防止数据未经授权的泄露和未被察觉的修改;
具有相当高的复杂性,使得破译的开销超过可能获得的利益,同时又要便于理解和掌握;
DES密码体制的安全性应该不依赖于算法的保密,其安全性仅以加密密钥的保密为基础;
实现经济,运行有效,并且适用于多种完全不同的应用。
1977年1月,美国政府颁布:采纳IBM公司设计的方案作为非机密数据的正式数据加密标准(DES Data Encryption Standard)。
DES全称为Data Encryption Standard,即数据加密标准,是一种使用密钥加密的块算法,1977年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),并授权在非密级政府通信中使用,随后该算法在国际上广泛流传开来。它基于使用56位密钥的对称算法。这个算法因为包含一些机密设计元素,相对短的密钥长度以及怀疑内含美国国家安全局(NSA)的后门而在开始时有争议,DES因此受到了强烈的学院派式的审查,并以此推动了现代的块密码及其密码分析的发展。
DES现在已经不是一种安全的加密方法,主要因为它使用的56位密钥过短。1999年1月,distributed.net与电子前哨基金会合作,在22小时15分钟内即公开破解了一个DES密钥。也有一些分析报告提出了该算法的理论上的弱点,虽然在实际中难以应用。为了提供实用所需的安全性,可以使用DES的派生算法3DES来进行加密,虽然3DES也存在理论上的攻击方法。在2001年,DES作为一个标准已经被高级加密标准(AES)所取代。另外,DES已经不再作为国家标准科技协会(前国家标准局)的一个标准。
DES算法简介
DES是一种典型的分组密码—一种将固定长度的明文通过一系列复杂的操作变成同样长度的密文的算法。对DES而言,块长度为64位。同时,DES使用密钥来自定义变换过程,因此算法认为只有持有加密所用的密钥的用户才能解密密文。密钥表面上是64位的,然而只有其中的56位被实际用于算法,其余8位可以被用于奇偶校验,并在算法中被丢弃。因此DES的有效密钥长度仅为56位。
DES设计中使用了分组密码设计的两个原则:混淆(confusion)和扩散(diffusion),其目的是抗击敌手对密码系统的统计分析。混淆是使密文的统计特性与密钥的取值之间的关系尽可能复杂化,以使密钥和明文以及密文之间的依赖性对密码分析者来说是无法利用的。扩散的作用就是将每一位明文的影响尽可能迅速地作用到较多的输出密文位中,以便在大量的密文中消除明文的统计结构,并且使每一位密钥的影响尽可能迅速地扩展到较多的密文位中,以防对密钥进行逐段破译。
DES加密的算法框架如下:
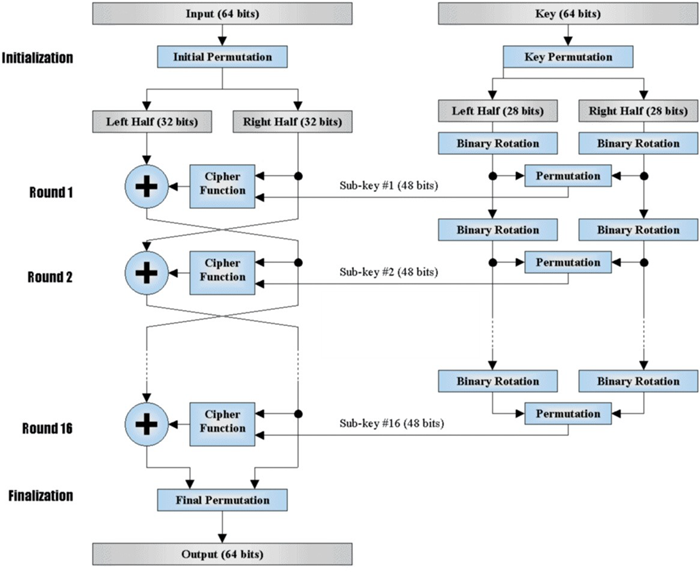
首先要生成一套加密密钥,从用户处取得一个64位长的密码口令,然后通过等分、移位、选取和迭代形成一套16个加密密钥,分别供每一轮运算中使用。
DES对64位(bit)的明文分组M进行操作,M经过一个初始置换IP,置换成m0。将m0明文分成左半部分和右半部分m0 = (L0,R0),各32位长。然后进行16轮完全相同的运算(迭代),这些运算被称为函数f,在每一轮运算过程中数据与相应的密钥结合。
在每一轮中,密钥位移位,然后再从密钥的56位中选出48位。通过一个扩展置换将数据的右半部分扩展成48位,并通过一个异或操作替代成新的48位数据,再将其压缩置换成32位。这四步运算构成了函数f。然后,通过另一个异或运算,函数f的输出与左半部分结合,其结果成为新的右半部分,原来的右半部分成为新的左半部分。将该操作重复16次。
经过16轮迭代后,左,右半部分合在一起经过一个末置换(数据整理),这样就完成了加密过程。
分组加密中的工作模式
分组加密算法是按分组大小来进行加解密操作的,如DES算法的分组是64位,而AES是128位,但实际明文的长度一般要远大于分组大小,这样的情况如何处理呢?这正是"mode of operation"即工作模式要解决的问题:明文数据流怎样按分组大小切分,数据不对齐的情况怎么处理等等。早在1981年,DES算法公布之后,NIST在标准文献FIPS 81中公布了4种工作模式:
电子密码本:Electronic Code Book Mode (ECB)
密码分组链接:Cipher Block Chaining Mode (CBC)
密文反馈:Cipher Feedback Mode (CFB)
输出反馈:Output Feedback Mode (OFB)
2001年又针对AES加入了新的工作模式:
计数器模式:Counter Mode (CTR)
后来又陆续引入其它新的工作模式,在此仅介绍几种常用的:
ECB:电子密码本模式(electronic codebook mode)
ECB模式只是将明文按分组大小切分,然后用同样的密钥正常加密切分好的明文分组。
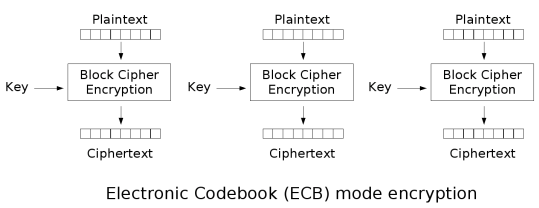
ECB的理想应用场景是短数据(如加密密钥)的加密。此模式的问题是无法隐藏原明文数据的模式,因为同样的明文分组加密得到的密文也是一样的。举例来说明:

从ECB的工作原理可以看出,如果明文数据在等分后,两块数据相同则会产生相同的加密数据块,这会辅助攻击者快速判断加密算法的工作模式,而将攻击资源聚集在破解某一块数据即可,一旦成功则意味着全文破解,大大提升了攻击效率。为了解决这一缺陷,设计者提出了更多的分组密码工作模式,这些模式下各组数据的加密过程彼此产生关联,尽最大可能混淆数据。
CBC:密码分组链接模式(cipher block chaining Triple)
此模式是1976年由IBM所发明,引入了IV(初始化向量:Initialization Vector)的概念。IV是长度为分组大小的一组随机,通常情况下不用保密,不过在大多数情况下,针对同一密钥不应多次使用同一组IV。 CBC要求第一个分组的明文在加密运算前先与IV进行异或;从第二组开始,所有的明文先与前一分组加密后的密文进行异或。(原理有没有和区块链(blockchain)一致,可以算是区块链的鼻祖)
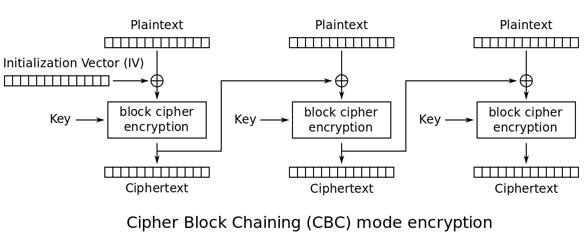
CBC模式相比ECB实现了更好的模式隐藏,但因为其将密文引入运算,加解密操作无法并行操作。同时引入的IV向量,还需要加、解密双方共同知晓方可。
CFB:密文反馈模式(Cipher FeedBack)
与CBC模式类似,但不同的地方在于,CFB模式先生成密码流字典,然后用密码字典与明文进行异或操作并最终生成密文。后一分组的密码字典的生成需要前一分组的密文参与运算。
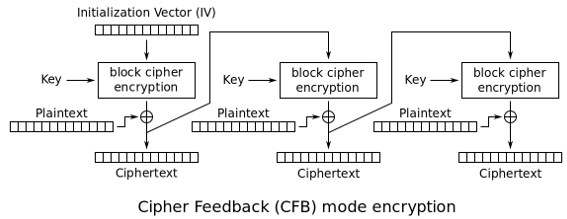
CFB模式是用分组算法实现流算法,明文数据不需要按分组大小对齐。
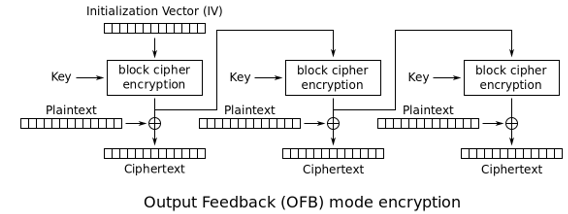
OFB:输出反馈模式(Output Feedbaek)
OFB模式与CFB模式不同的地方是:生成字典的时候会采用明文参与运算,CFB采用的是密文。
CTR:计数器模式(counter mode)
上面的几种工作模式都存在一个共性:数据块彼此之间关联,当前块的解密依赖前面的密文块,因此不能随机访问任意加密块。这样会使得用户为了获取其中一点数据而不得不解密所有数据,当数据量大时效率较低。
CTR模式同样会产生流密码字典,但同是会引入一个计数,以保证任意长时间均不会产生重复输出。
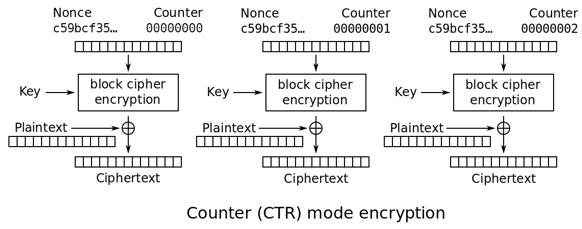
CTR模式只需要实现加密算法以生成字典,明文数据与之异或后得到密文,反之便是解密过程。CTR模式可以采用并行算法处理以提升吞量,另外加密数据块的访问可以是随机的,与前后上下文无关。
CCM:Counter with CBC-MAC
CCM模式,全称是Counter with Cipher Block Chaining-Message Authentication Code,是CTR工作模式和CMAC认证算法的组合体,可以同时数据加密和鉴别服务。
明文数据通过CTR模式加密成密文,然后在密文后面再附加上认证数据,所以最终的密文会比明文要长。具体的加密流程如下描述:先对明文数据认证并产生一个tag,在后续加密过程中使用此tag和IV生成校验值U。然后用CTR模式来加密原输入明文数据,在密文的后面附上校验码U。
GCM:伽罗瓦计数器模式
类型CCM模式,GCM模式是CTR和GHASH的组合,GHASH操作定义为密文结果与密钥以及消息长度在GF(2^128)域上相乘。GCM比CCM的优势是在于更高并行度及更好的性能。TLS 1.2标准使用的就是AES-GCM算法,并且Intel CPU提供了GHASH的硬件加速功能
补充信息
与分组密码相对应的便是序列密码,又称流密码,是指利用密钥通过复杂的密码算法产生大量的伪随机位流,对明文数据流进行加密。在进行解密时,用同样的密钥和算法产生相同的伪随机位流,用以还原明文数据流。目前,公开的序列密码算法主要有RC4、SEAL等。序列密码以一个元素(一个字母或一个比特)作为基本的处理单元,具有转换速度快、低错误传播的优点,硬件实现简单;但加密结果混淆度低、且数据的小幅度变化敏感性低,即插入修改较少的数据,加密结果不会发生大幅变化,这样会给攻击者提供较多分析素材。
总结
ECB是不推荐的方式,Key相同时,相同的明文在不同的时候产生相同的明文,容易遭到字典攻击,CBC由于加入了向量参数,一定程度上抵御了字典工具,但缺点也随之而来,一旦中间一个数据出错或丢失,后面的数据将受到影响,CFB与CBC类似,好处是明文和密文不用是8bit的整数倍,中间一个数据出错,只影响后面的几个块的数据,OFB比CFB方式,一旦一个数据出错,不会影响后面的数据,但安全性降低;因此,推荐使用CFB方式,但每个数据包单独加密,否则一个数据包丢失,需要做很多容错处理;当然,具体问题也要具体分析,对于只需要“特定安全性”,不需要“计算安全性”以上的软件,也可以使用ECB模式,与其它块密码相似,DES自身并不是加密的实用手段,而必须以某种工作模式进行实际操作。
参考链接:
https://github.com/matt-wu/AES
http://www.freebuf.com/articles/database/130521.html
分组加密中的填充算法
在分组加密算法中(例如DES),我们首先要将原文进行分组,然后每个分组进行加密,然后组装密文。其中有一步是分组。如何分组?假设我们现在的数据长度是24字节,BlockSize是8字节,那么很容易分成3组,一组8字节,如果现有的待加密数据不是BlockSize的整数倍,那该如何分组?
例如,有一个17字节的数据,BlockSize是8字节,怎么分组?我们可以对原文进行填充(padding),将其填充到8字节的整数倍。假设使用PKCS#5进行填充(以下都是以PKCS#5为示例),BlockSize是8字节(64bit):
待加密数据原长度为1字节:0x41
填充后:0x410x070x070x070x070x070x070x07
待加密数据原长度为2字节:0x410x41
填充后:0x410x410x060x060x060x060x060x06
待加密数据原长度为3字节:0x410x410x41
填充后:0x410x410x410x050x050x050x050x05
待加密数据原长度为4字节:0x410x410x410x41
填充后:0x410x410x410x410x040x040x040x04
待加密数据原长度为5字节:0x410x410x410x410x41
填充后:0x410x410x410x410x410x030x030x03
待加密数据原长度为6字节:0x410x410x410x410x410x41
填充后:0x410x410x410x410x410x410x020x02
待加密数据原长度为7字节:0x410x410x410x410x410x410x41
填充后:0x410x410x410x410x410x410x410x01
待加密数据原长度为8字节:0x410x410x410x410x410x410x410x41
填充后:0x410x410x410x410x410x410x410x410x080x080x080x080x080x080x080x08
为啥当为整数倍时,还是要多增加8个0x08?假设当x是8的整数倍时,不多填充8个0x08:当解密后时,我看到了解密后的数据的末尾的最后一个字节,这个字节恰好是0x01,那你说,这个字节是填充上去的呢?还是实际的数据呢?
PKCS5Padding与PKCS7Padding的区别
PKCS5Padding与PKCS7Padding基本上是可以通用的。在PKCS5Padding中,明确定义Block的大小是8位,而在PKCS7Padding定义中,对于块的大小是不确定的,可以在1-255之间,填充值的算法都是一样的:
pad = k - (l mod k) //k=块大小,l=数据长度,如果k=8, l=9,则需要填充额外的7个byte的7
可以得出:Pkcs5是Pkcs7的特例(Block的大小始终是8位)。当Block的大小始终是8位的时候,Pkcs5和Pkcs7是一样的。
DES与3DES
3DES(即Triple DES)是DES向AES过渡的加密算法,它使用3条56位的密钥对数据进行三次加密,是DES的一个更安全的变形。它以DES为基本模块,通过组合分组方法设计出分组加密算法。比起最初的DES,3DES更为安全。该方法使用两个密钥,执行三次DES算法,加密的过程是加密-解密-加密,解密的过程是解密-加密-解密。
3DES加密过程为:C=Ek3(Dk2(Ek1(P)))
3DES解密过程为:P=Dk1(EK2(Dk3(C)))
采用两个密钥进行三重加密的好处有:
两个密钥合起来有效密钥长度有112bit,可以满足商业应用的需要,若采用总长为168bit的三个密钥,会产生不必要的开销。
加密时采用加密-解密-加密,而不是加密-加密-加密的形式,这样有效的实现了与现有DES系统的向后兼容问题。因为当K1=K2时,三重DES的效果就和原来的DES一样,有助于逐渐推广三重DES。
三重DES具有足够的安全性,目前还没有关于攻破3DES的报道。
AES
上文的数据加密标准(Data Encryption Standard: DES)的密钥长度是56比特,因此算法的理论安全强度是256。但二十世纪中后期正是计算机飞速发展的阶段,元器件制造工艺的进步使得计算机的处理能力越来越强,DES将不能提供足够的安全性。1997年1月2号,美国国家标准技术研究所(National Institute of Standards and Technology: NIST)宣布希望征集高级加密标准(Advanced Encryption Standard: AES),用以取代DES。AES评判要求:
NIST在征集算法的时候就提出了几项硬性要求:
分组加密算法:支持128位分组大小,128/192/256位密钥
安全性不低于3DES,但实施与执行要比3DES的更高效
优化过的ANSI C的实现代码
KAT(Known-Answer tests)及MCT(Monte Carlo Tests)测试及验证
软件及硬件实现的便捷
可抵御已知攻击
AES得到了全世界很多密码工作者的响应,先后有很多人提交了自己设计的算法。第一轮共有15种算法入选,其中5种算法入围了决赛,分别是:Rijndael,Serpent,Twofish,RC6和MARS。又经过3年的验证、评测及公众讨论之后Rijndael算法最终入选。Rijndael是一个分组密码算法族,由比利时学者Joan Daemen和Vincent Rijmen所提出的,算法的名字就由两位作者的名字组合而成。其分组长度包括128比特、160比特、192比特、224比特、256比特,密钥长度也包括这五种长度,但是最终AES只选取了分组长度为128比特,密钥长度为128比特、192比特和256比特的三个版本。
Rijndael的优势在于集安全性、性能、效率、可实现性及灵活性与一体。Rijndael设计思想:
安全性(Security) 算法足够强,抗攻击
经济性(Efficiency) 算法运算效率高
密钥捷变(Key Agility) 更改密钥所引入的损失尽量小,即最小消耗的密钥扩展算法
适应性 (Versatility) 适用于不同的CPU架构,软件或硬件平台的实现
设计简单(Simplicity) 轮函数的设计精简,只是多轮迭代
AES的算法原理
加密算法的一般设计准则
混淆 (Confusion) 最大限度地复杂化密文、明文与密钥之间的关系,通常用非线性变换算法达到最大化的混淆。
扩散 (Diffusion) 明文或密钥每变动一位将最大化地影响密文中的位数,通常采用线性变换算法达到最大化的扩散。
对Rijndael算法来说解密过程就是加密过程的逆向过程。下图为AES加解密的流程,从图中可以看出:1)解密算法的每一步分别对应加密算法的逆操作,2)加解密所有操作的顺序正好是相反的。正是由于这几点(再加上加密算法与解密算法每步的操作互逆)保证了算法的正确性。
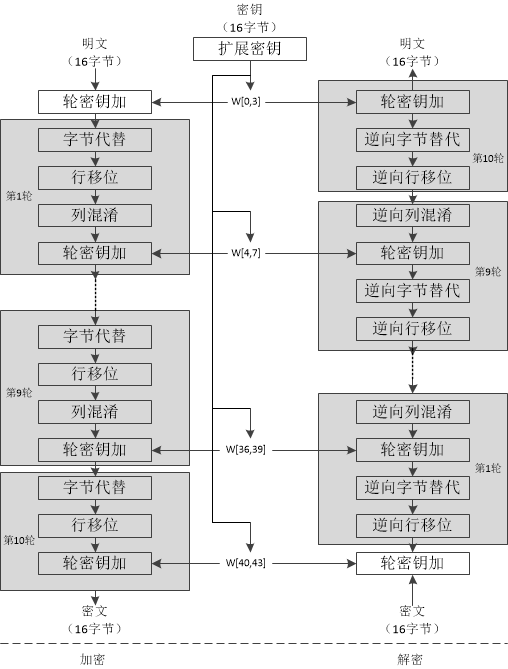
Rijndael算法是基于代换-置换网络(SPN,Substitution-permutation network)的迭代算法。明文数据经过多轮次的转换后方能生成密文,每个轮次的转换操作由轮函数定义。轮函数任务就是根据密钥编排序列(即轮密码)对数据进行不同的代换及置换等操作。
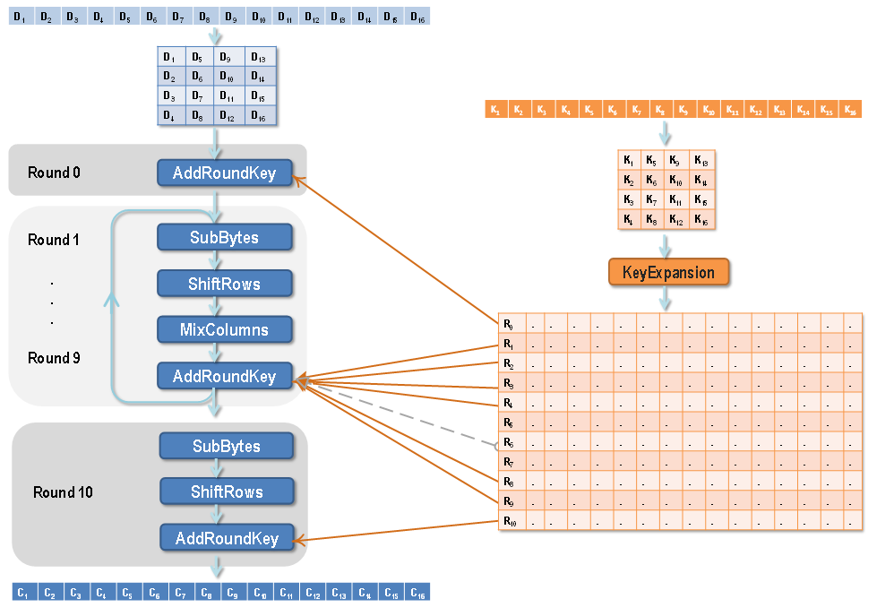
图左侧为轮函数的流程,主要包含4种主要运算操作:字节代换(SubByte)、行移位(ShiftRow)、列混合(MixColumn)、轮密钥加(AddRoundKey)。
图右侧为密钥编排方案,在Rijndael中称为密钥扩展算法(KeyExpansion)。
轮函数
我们已经得知轮函数主要包含4种运算,但不同的运算轮所做的具体运的算组合并不相同。主要区别是初始轮(Round: 0)和最后一轮(Round: Nr),所有中间轮的运算都是相同的,会依次进行4种运算,即:
字节代换(SubByte)
行移位(ShiftRow)
列混合(MixColumn)
轮密钥加(AddRoundKey)
Rijndael算法支持大于128位的明文分组,所以需要列数更多的矩阵来描述。Rijndael轮函数的运算是在特殊定义的有限域GF(256)上进行的。有限域(Finite Field)又名伽罗瓦域(Galois field),简单言之就是一个满足特定规则的集合,集合中的元素可以进行加减乘除运算,且运算结果也是属于此集合。根据Rinjdael算法的定义,加密轮数会针对不同的分组及不同的密钥长度选择不同的数值:
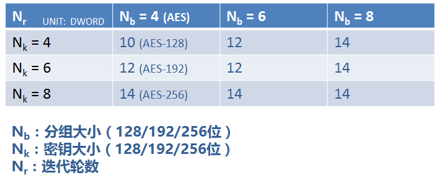
AES标准只支持128位分组(Nb = 4)的情况。AES标准算法将128位的明文,以特定次序生成一个4×4的矩阵(每个元素是一个字节,8位),即初始状态(state),经由轮函数的迭代转换之后又将作为下一轮迭代的输入继续参与运算直到迭代结束。
轮函数拆解:字节代换(Substitute Bytes)
字节代换(SubBytes)是对state矩阵中的每一个独立元素于置换盒(Substitution-box,S盒)中进行查找并以此替换输入状态的操作。字节代换是可逆的非线性变换,也是AES运算组中唯一的非线性变换。字节代换逆操作也是通过逆向置换盒的查找及替换来完成的,主要功能是通过S盒完成一个字节到另外一个字节的映射。
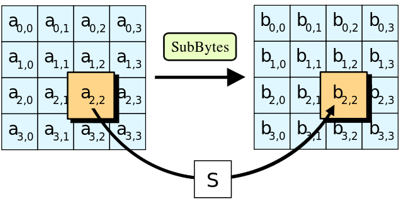
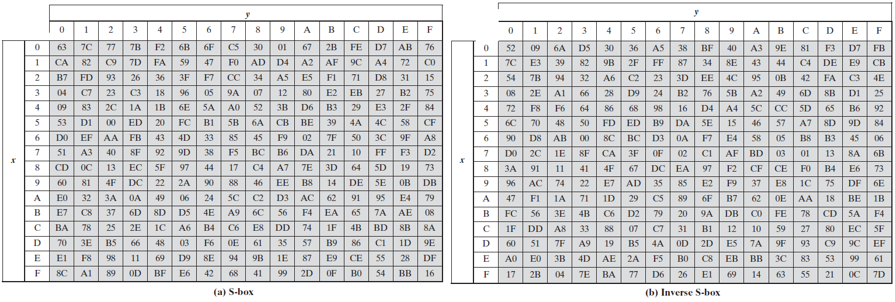
S盒是由一个有限域GF(256)上的乘法求逆并串联线性仿射变换所构造出来的,不是一个随意构造的简单查询表。S因其运算复杂,众多的AES 软件及硬件实现直接使用了查找表(LUP, Look-up table),但查询表的方式并不适合所有场景,针对特定的硬件最小化面积设计需求,则要采用优化的组合逻辑以得到同价的S盒替换。盒是事先设计好的16×16的查询表,即256个元素。S盒用于提供密码算法的混淆性。S盒的详细构造方法可以参考文献。这里直接给出构造好的结果,下图(a)为S盒,图(b)为S-1(S盒的逆)。S和S-1分别为16×16的矩阵,完成一个8比特输入到8比特输出的映射,输入的高4-bit对应的值作为行标,低4-bit对应的值作为列标。
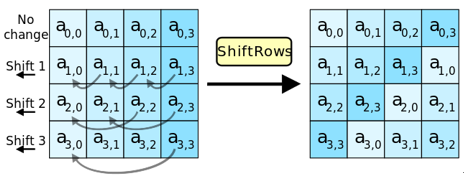
轮函数拆解:行移位(Shift Rows)
行移位主要目的是实现字节在每一行的扩散,属于线性变换。行移位是一个4×4的矩阵内部字节之间的置换,用于提供算法的扩散性。
1) 正向行移位
正向行移位用于加密,其原理图如下。其中:第一行保持不变,第二行循环左移8比特,第三行循环左移16比特,第四行循环左移24比特。假设矩阵的名字为state,用公式表示如下:state[i][j] = state[i][(j+i)%4];其中i、j属于[0,3]。
2) 逆向行移位
逆向行移位即是相反的操作,即:第一行保持不变,第二行循环右移8比特,第三行循环右移16比特,第四行循环右移24比特。用公式表示如下:state’[i][j] = state[i][(4+j-i)%4];其中i、j属于[0,3]。
轮函数拆解:列混合(Mix Columns)
列混合是通过将state矩阵与常矩阵C相乘以达成在列上的扩散,属于代替变换。列混合是Rijndael算法中最复杂的一步,其实质是在有限域GF(256)上的多项式乘法运算。
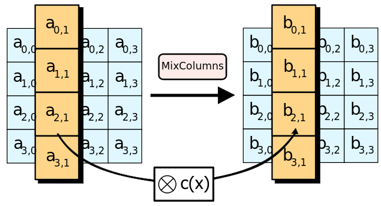
1) 正向列混淆
正向列混淆的原理图如下:
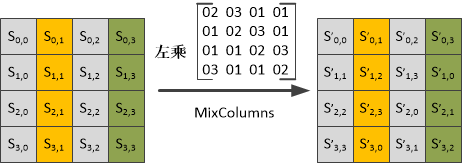
根据矩阵的乘法可知,在列混淆的过程中,每个字节对应的值只与该列的4个值有关系。此处的乘法和加法都是定义在GF(28)上的,需要注意如下几点:
将某个字节所对应的值乘以2,其结果就是将该值的二进制位左移一位,如果原始值的最高位为1,则还需要将移位后的结果异或00011011;
乘法对加法满足分配率,例如:07·S0,0=(01⊕02⊕04)·S0,0= S0,0⊕(02·S0,0)(04·S0,0)
此处的矩阵乘法与一般意义上矩阵的乘法有所不同,各个值在相加时使用的是模28加法(异或运算)。
下面举一个例子,假设某一列的值如下图,运算过程如下:
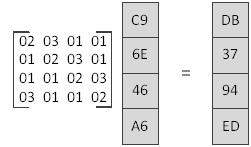

在计算02与C9的乘积时,由于C9对应最左边的比特为1,因此需要将C9左移一位后的值与(0001 1011)求异或。同理可以求出另外几个值。
2) 逆向列混淆
逆向列混淆的原理图如下:
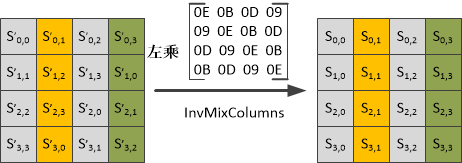
由于:

说明两个矩阵互逆,经过一次逆向列混淆后即可恢复原文。
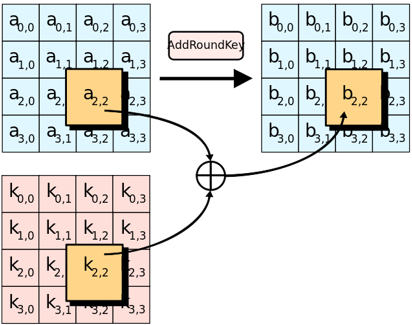
轮函数拆解:轮密钥加(Add Round Key)
密钥加是将轮密钥简单地与状态进行逐比特异或。这个操作相对简单,其依据的原理是“任何数和自身的异或结果为0”。加密过程中,每轮的输入与轮子密钥异或一次;因此,解密时再异或上该轮的轮子密钥即可恢复。
密钥扩展算法(Key Expansion)
AES加解密中每轮的密钥分别由种子密钥经过密钥扩展算法得到。算法中16字节的明文、密文和轮子密钥都以一个4×4的矩阵表示。
密钥扩展算法是Rijndael的密钥编排实现算法,其目的是根据种子密钥(用户密钥)生成多组轮密钥。轮密钥为多组128位密钥,对应不同密钥长度,分别是11,13,15组。
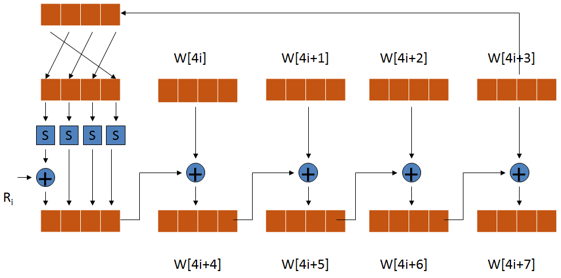
密钥扩展的原理图如下:
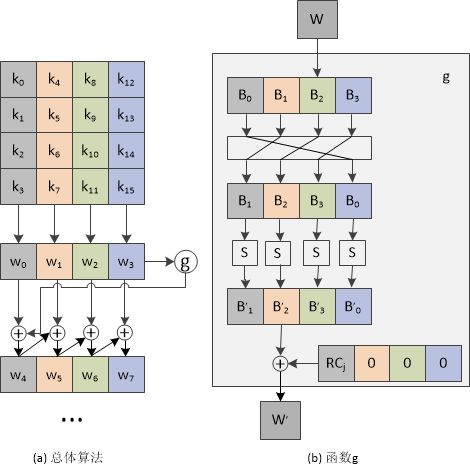
密钥扩展过程说明:
1) 将种子密钥按图(a)的格式排列,其中k0、k1、……、k15依次表示种子密钥的一个字节;排列后用4个32比特的字表示,分别记为w[0]、w[1]、w[2]、w[3];
2) 按照如下方式,依次求解w[j],其中j是整数并且属于[4,43];
3) 若j%4=0,则w[j]=w[j-4]⊕g(w[j-1]),否则w[j]=w[j-4]⊕w[j-1];
函数g的流程说明:
a) 将w循环左移8比特;
b) 分别对每个字节做S盒置换;
c) 与32比特的常量(RC[j/4],0,0,0)进行异或,RC是一个一维数组,其值如下。(RC的值只需要有10个,而此处用了11个,实际上RC[0]在运算中没有用到,增加RC[0]是为了便于程序中用数组表示。由于j的最小取值是4,j/4的最小取值则是1,因此不会产生错误。)
RC = {0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36}
动画演示加密过程:
Enrique Zabala创建了一个AES-128加密算法的动画演示,清楚、直观地介绍了轮函数执行的过程。
波士顿大学的Howard Straubing做了这么一个动画来展示AES加密算法的演示。
参考链接:
https://github.com/matt-wu/AES/
其他参考资料:
AES算法的使用
在正式软件运用中并不推荐自己编写代码,很多开源项目如Linux,OPENSSL,SRTP等都有非常高效的实现。由于是分组加密,所以在使用的时候设定分组加密工作模式和填充算法。
Blowfish
Blowfish是一个对称密钥加密分组密码算法,由布鲁斯·施奈尔于1993年设计,现已应用在多种加密产品。Blowfish算法由于分组长度太小已被认为不安全,施奈尔更建议在现代应用中使用Twofish密码。
施奈尔设计的Blowfish算法用途广泛,意在替代老旧的DES及避免其他算法的问题与限制。Blowfish刚刚研发出的时候,大部分其他加密算法是专利所有的或属于商业(政府)机密,所以发展起来非常受限制。施奈尔则声明Blowfish的使用没有任何限制,任何国家任何人任何时候都可以随意使用Blowfish算法。
Blowfish主要包括关键的几个S盒和一个复杂的核心变换函数。
Bcrypt
bcrypt是一个由Niels Provos以及David Mazières根据Blowfish加密算法所设计的密码散列函数,于1999年在USENIX中展示。实现中bcrypt会使用一个加盐的流程以防御彩虹表攻击,同时bcrypt还是适应性函数,它可以借由增加迭代之次数来抵御日益增进的电脑运算能力透过暴力法破解。
由bcrypt加密的文件可在所有支持的操作系统和处理器上进行转移。它的口令必须是8至56个字符,并将在内部被转化为448位的密钥。然而,所提供的所有字符都具有十分重要的意义。密码越强大数据就越安全。
除了对数据进行加密,默认情况下,bcrypt在删除数据之前将使用随机数据三次覆盖原始输入文件,以阻挠可能会获得您的计算机数据的人恢复数据的尝试。如果不想使用此功能,可设置禁用此功能。
具体来说,bcrypt使用保罗·柯切尔的算法实现,随bcrypt一起发布的源代码对原始版本作了略微改动。
使用参考案例
Dropbox账户密码存储实践
众所周知,存储明文密码是一件很糟糕的事情。如果数据库存储了明文密码,一旦数据泄漏,那么用户账号就危险了。因为这个原因,早在1976年,工业界就提出了一套使用单向哈希机制来安全地存储密码的标准(从Unix Crypt开始)。很不幸的是,尽管这种方式可以阻止你直接读取到密码,但是所有的哈希机制都不能阻止攻击者在离线环境下暴力破解它,攻击者只需要遍历一个可能包含正确密码的列表,对每个可能的密码进行哈希然后跟获取到的密码(使用哈希机制存储的密码)比对即可。在这种环境下,安全哈希函数如SHA在用于密码哈希的时候有一个致命的缺陷,那就是它们运算起来太快了。一个现代的商用CPU一秒钟可以生成数百万个SHA256哈希值。一些特殊的GPU集群的计算速度甚至可以达到每秒数十亿次。
过去的这些年,为了应对攻击,Dropbox对密码哈希方法进行了数次升级。他们的密码存储方案依赖三个不同层级的密码保护,如下图所示:
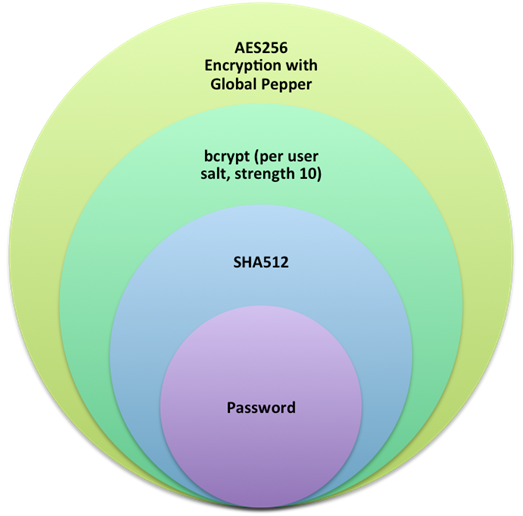
Dropbox采用 Bcrypt 作为核心哈希算法,每个用户都有一个独立的salt以及一个加密的key(这个key也可以是一个全局的,通常也叫pepper),salt和key是分开存储的。与基础的 Bcrypt 算法在一些重要的方面是不同的:
首先,用户的明文密码通过 SHA512 算法转换成了一个哈希值。这一步主要是针对Bcrypt的两个突出的问题。有些Bcrypt的实现中会将用户输入截取为72个字节大小以降低密码熵,而另外有一些实现并没有截取用户输入导致其容易受到DoS攻击,因为它们允许任意长度的密码输入。通过使用SHA,可以快速的将一些的确很长的密码转换为一个512比特的固定长度,解决了上述两个问题,即避免降低密码熵和预防DoS攻击。
然后,对SHA512哈希后的值使用bcrypt算法再次哈希,使用的工作因子是10,每个用户都有一个单独的salt。不像其他的哈希算法比如SHA等,Bcrypt算法很慢,它很难通过硬件和GPU加速。设置工作因子为10,在服务器上执行一次bcrypt大概需要100毫秒。
最后,使用Bcrypt哈希过后的结果再次使用AES256算法进行加密,使用的密钥是所有用户统一的,称之为pepper。pepper是基于深度考量的一种防御措施,pepper以一种攻击者难以发现的方式存储起来(比如不要放在数据库的表中)。由此,如果只是密码被拖库了,通过AES256加密过的哈希密码对于攻击者来说毫无用处。
为什么不使用scrypt或argon2?
Dropbox曾考虑过使用Scrypt,但是我们对Dropbox有更多的经验。关于这几种算法哪种更好的讨论一直都有,大部分的安全领域的专家都认为scrypt和bcrypt的安全性上相差无几。
Dropbox考虑在下一次升级中使用argon2算法:因为在采用当前的方案的时候,argon2还没有赢得 Password Hashing Competition。此外,从1999年以来,Bcrypt还没有发现有任何重大的攻击存在。
为什么使用一个全局的密钥(pepper)替代哈希函数
如前面提到的,采用一个全局的密钥是我们深度权衡后的一个防御措施,而且,pepper是单独存储的。但是,单独存储pepper也意味着要考虑pepper泄露的可能性。如果只是用pepper对密码进行哈希,那么一旦pepper泄露,无法从哈希后的结果反解得到之前bcrypt哈希过的密码值。作为一个替代方案,Dropbox使用了AES256加密算法。AES256算法提供了差不多的安全性,同时还可以反解回原来的值。尽管AES256这个加密函数的输入是随机的,Dropbox还是额外加上了一个随机的初始化向量(IV)来增强安全性。下一步,Dropbox考虑将pepper存储到一个硬件安全模块(HSM),这虽然是一个相当复杂的任务,但是它能极大的降低pepper泄露的风险。同时,也计划在下一次升级中增强Bcrypt的强度。
展望
Dropbox相信使用SHA512,加上bcrypt和AES256是当前保护密码最稳妥和流行的方法之一。同时所谓道高一尺魔高一丈。密码哈希程序只是加固Dropbox的众多举措之一,Dropbox还部署了额外的保护措施-比如针对暴力攻击者密码尝试次数的速度限制,验证码,以及其他一些方法等。
原文链接:How Dropbox securely stores your passwords
用户密码加密存储问答
我们数据库的权限管理十分严格,敏感信息开发工程师都看不到,密码明文存储不行吗?
不行。存储在数据库的数据面临很多威胁,有应用程序层面、数据库层面的、操作系统层面的、机房层面的、员工层面的,想做到百分百不被黑客窃取,非常困难。如果密码是加密之后再存储,那么即便被拖库,黑客也难以获取用户的明文密码。可以说,密码加密存储是用户账户系统的底线,它的重要性,相当于独自出远门时缝在内衣里钱,虽然用到他们的概率不大,但关键时刻能救命。
那用加密算法比如AES,把密码加密下再存,需要明文的时候我再解密。
不行。这涉及到怎么保存用来加密解密的密钥,虽然密钥一般跟用户信息分开存储,且业界也有一些成熟的、基于软件或硬件的密钥存储方案。但跟用户信息的保存一样,想要密钥百分百不泄露,不可能做到。用这种方式加密密码,能够降低黑客获取明文密码的概率。但密钥一旦泄露,用户的明文密码也就泄露了,不是一个好方法。另外用户账户系统不应该保存用户的明文密码,在用户忘记密码的时候,提供重置密码的功能而不是找回密码。
保存所有密码的HASH值,比如MD5。是不是就可以了?
不是所有的HASH算法都可以,准确讲应该是Cryptographic Hash。Cryptographic Hash具有如下几个特点:
给定任意大小任意类型的输入,计算hash非常快;
给定一个hash,没有办法计算得出该hash所对应的输入;
对输入做很小改动,hash就会发生很大变化;
没有办法计算得到两个hash相同的输入;
虽然不是为加密密码而设计,但其第2、3、4三个特性使得Cryptographic Hash非常适合用来加密用户密码。常见的Cryptographic Hash有MD5、SHA-1、SHA-2、SHA-3/Keccak、BLAKE2。从1976年开始,业界开始使用Cryptographic Hash加密用户密码,最早见于Unix Crypt。但MD5、SHA-1已被破解,不适合再用来保存密码。
那我保存用户密码的SHA256值。
不行。黑客可以用查询表或彩虹表来破解用户密码。注意是破解密码不是破解sha256,能根据sha256破解密码的原因是,用户密码往往需要大脑记忆、手工输入,所以不会太复杂,往往具有有限的长度、确定的取值空间。
短的取值简单的密码可以用查询表破解
比如8位数字密码,一共只有10^8=100000000种可能。一亿条数据并不算多,黑客可以提前吧0-99999999的sha256都计算好,并以sha256做key密码为value存储为一个查询表,当给定sha256需要破解时,从表中查询即可。
取值相对复杂,且长度较长的密码,可以用彩虹表破解
比如10位,允许数字、字母大小写的密码,一共有(10+26+26)^10~=84亿亿种可能,记录非常之多难以用查询表全部保存起来。这时候黑客会用一种叫做彩虹表的技术来破解,彩虹表用了典型的计算机世界里解决问题的思路,时间空间妥协。在这个例子里面,空间不够,那就多花一些时间。在彩虹表中,可以将全部的sha256值转化为长度相同的若干条hash链,只保存hash链的头和尾,在破解的时候先查询得到sha256存在于哪条hash链中,然后计算这一条hash链上的所有sha256,通过实时比对来破解用户密码。

上图图展示了一个hash链长度为3的彩虹表,因为在hash链中需要将hash值使用R函数映射回密码取值空间,为了降低R函数的冲突概率,长度为K的hash链中,彩虹表会使用k个R函数,因为每次迭代映射回密码空间使用的R函数不一样,这种破解方法被称作彩虹表攻击。
实际的情况Hash链要比远比上例更长,比如我们的例子中全部的84亿亿个sha256存不下,可以转化为840亿条长度为1千万的sha链。对彩虹表原理感兴趣的话,可以阅读它的维基百科。
网路上甚至有一些已经计算好的彩虹表可以直接使用,所以直接保存用户密码的sha256是非常不安全的。
怎样避免彩虹表攻击?
简单讲,就是加盐。一般来讲用户密码是个字符串key、盐是我们生成的字符串salt。原来我们保存的是key的hash值HASH(key),现在我们保存key和salt拼接在一起的hash值HASH(key+salt)。这样黑客提前计算生成的彩虹表,就全都失效了。
盐应该怎么生成,随机生成一个字符串?
这是个好问题,并不是加个盐就安全了,盐的生成有很多讲究。
使用CSPRNG(Cryptographically Secure Pseudo-Random Number Generator)生成盐,而不是普通的随机数算法;CSPRNG跟普通的随机数生成算法,比如C语言标准库里面的rand()方法,有很大不同。正如它的名字所揭示,CSPRNG是加密安全的,这意味着用它产生的随机数更加随机,且不可预测。常见编程语言都提供了CSPRNG,如下表:
编程语言:CSPRNG
C/C++:CryptGenRandom
Java:Java.security.SecureRandom
PHP:mcrypt_create_iv
Erlang:Crypt:strong_rand_bytes
Linux/Unix上的任何编程语言:读取/dev/random
盐不能太短
想想查询表和彩虹表的原理,如果盐很短,那意味着密码+盐组成的字符串的长度和取值空间都有限。黑客完全可以为密码+盐的所有组合建立彩虹表。
盐不能重复使用
如果所有用户的密码都使用同一个盐进行加密。那么不管盐有多复杂、多大的长度,黑客都可以很容易的使用这个固定盐重新建立彩虹表,破解你的所有用户的密码。如果你说,我可以把固定盐存起来,不让别人知道啊,那么你应该重新读一下我关于为什么使用AES加密不够安全的回答。即便你为每一个用户生成一个随机盐,安全性仍然不够,因为这个盐在用户修改密码时重复使用了。应当在每一次需要保存新的密码时,都生成一个新的盐,并跟加密后的hash值保存在一起。
注意:有些系统用一个每个用户都不同的字段,uid、手机号、或者别的什么,来作为盐加密密码。这不是一个好主意,这几乎违背了上面全部三条盐的生成规则。
那我自己设计一个黑客不知道的HASH算法,这样你的那些破解方法就都失效了。
不可以。首先如果你不是一个密码学专家,你很难设计出一个安全的hash算法。不服气的话,你可以再看一遍上面我关于Cryptographic Hash的描述,然后想一想自己怎么设计一个算法可以满足它的全部四种特性。就算你是基于已有的Cryptographic Hash的基础上去设计,设计完之后,也难以保证新算法仍然满足Cryptographic Hash的要求。而一旦你的算法不满足安全要求,那么你给了黑客更多更容易破解用户密码的方法。
即便你能设计出一个别人不知道的Cryptographic Hash算法,你也不能保证黑客永远都不知道你的算法。黑客往往都有能力访问你的代码,想想柯克霍夫原则或者香农公里:
密码系统应该就算被所有人知道系统的运作步骤,仍然是安全的。
为每一个密码都加上不同的高质量的盐,做HASH,然后保存。这样可以了吧?
以前是可以的,现在不行了。计算机硬件飞速发展,一个现代通用CPU能以每月数百万次的速度计算sha256,而GPU集群计算sha256,更是可以达到每秒10亿次以上。这使得暴力破解密码成为可能,黑客不再依赖查询表或彩虹表,而是使用定制过的硬件和专用算法,直接计算每一种可能,实时破解用户密码。
那怎么办呢?回想上面关于Cryptographic Hash特性的描述,其中第一条:
给定任意大小任意类型的输入,计算hash非常快
Cryptographic Hash并不是为了加密密码而设计的,它计算非常快的这个特性,在其他应用场景中非常有用,而在现在的计算机硬件条件下,用来加密密码就显得不合适了。针对这一点,密码学家们设计了PBKDF2、BCRYPT、SCRYPT等用来加密密码的Hash算法,称作Password Hash。在他们的算法内部,通常都需要计算Cryptographic Hash很多次,从而减慢Hash的计算速度,增大黑客暴力破解的成本。可以说Password Hash有一条设计原则,就是计算过程能够按要求变慢,并且不容易被硬件加速。
应该使用哪一种Password Hash?
PBKDF2、BCRYPT、SCRYPT曾经是最常用的三种密码Hash算法,至于哪种算法最好,多年以来密码学家们并无定论。但可以确定的是,这三种算法都不完美,各有缺点。其中PBKDF2因为计算过程需要内存少所以可被GPU/ASIC加速,BCRYPT不支持内存占用调整且容易被FPGA加速,而SCRYPT不支持单独调整内存或计算时间占用且可能被ASIC加速并有被旁路攻击的可能。
2013年NIST(美国国家标准与技术研究院)邀请了一些密码学家一起,举办了密码hash算法大赛(Password Hashing Competition),意在寻找一种标准的用来加密密码的hash算法,并借此在业界宣传加密存储用户密码的重要性。大赛列出了参赛算法可能面临的攻击手段:
加密算法破解(原值还原、哈希碰撞等,即应满足Cryptographic Hash的第2、3、4条特性);
查询表/彩虹表攻击;
CPU优化攻击;
GPU、FPGA、ASIC等专用硬件攻击;
旁路攻击。
最终在2015年7月,Argon2算法赢得了这项竞赛,被NIST认定为最好的密码hash算法。不过因为算法过新,目前还没听说哪家大公司在用Argon2做密码加密。
网络安全通信中要用到两类密码算法,一类是对称密码算法,另一类是非对称密码算法。对称密码算法的加密密钥能够从解密密钥中推算出来,反过来也成立。在大多数对称算法中,加密解密密钥是相同的。它要求发送者和接收者在安全通信之前,商定一个密钥。对称算法的安全性依赖于密钥,泄漏密钥就意味着任何人都能对消息进行加密解密。只要通信需要保密,密钥就必须保密。

对称算法又可分为两类。一次只对明文中的单个位(有时对字节)运算的算法称为序列算法或序列密码。另一类算法是对明文的一组位进行运算,这些位组称为分组,相应的算法称为分组算法或分组密码。现代计算机密码算法的典型分组长度为64位――这个长度既考虑到分析破译密码的难度,又考虑到使用的方便性。后来,随着破译能力的发展,分组长度又提高到128位或更长。
常用的采用对称密码术的加密方案有5个组成部分:
明文:原始信息。
加密算法:以密钥为参数,对明文进行多种置换和转换的规则和步骤,变换结果为密文。
密钥:加密与解密算法的参数,直接影响对明文进行变换的结果。
密文:对明文进行变换的结果。
解密算法:加密算法的逆变换,以密文为输入、密钥为参数,变换结果为明文。
对称密码当中有几种常用到的数学运算。这些运算的共同目的就是把被加密的明文数码尽可能深地打乱,从而加大破译的难度。
移位和循环移位:移位就是将一段数码按照规定的位数整体性地左移或右移。循环右移就是当右移时,把数码的最后的位移到数码的最前头,循环左移正相反。例如对十进制数码12345678循环右移1位(十进制位)的结果为81234567,而循环左移1位的结果则为23456781。
置换:就是将数码中的某一位的值根据置换表的规定,用另一位代替。它不像移位操作那样整齐有序,看上去杂乱无章。这正是加密所需,被经常应用。
扩展:就是将一段数码扩展成比原来位数更长的数码。扩展方法有多种,例如,可以用置换的方法,以扩展置换表来规定扩展后的数码每一位的替代值。
压缩:就是将一段数码压缩成比原来位数更短的数码。压缩方法有多种,例如,也可以用置换的方法,以表来规定压缩后的数码每一位的替代值。
异或:这是一种二进制布尔代数运算。也可以简单地理解为,参与异或运算的两数位如相等,则结果为0,不等则为1。异或的数学符号为⊕。
迭代:迭代就是多次重复相同的运算,这在密码算法中经常使用,以使得形成的密文更加难以破解。
常见的对称加密算法有AES、ChaCha20、3DES、Salsa20、DES、Blowfish、IDEA、RC5、RC6、Camellia。对称加密的速度比公钥加密快很多,在很多场合都需要对称加密。
RC4
假设定义RC4的运算过程是rc4(key,data),那么密文=rc4(key,明文),明文=rc4(key,密文)。所以对一段数据迭代地做奇数次RC4运算,就得到密文,对这段数据迭代地做偶数次RC4运算,结果依旧是原来的那段数据。
这种对称性就是基于密钥流的加密算法的一个特征。RC4加密算法也是一种基于密钥流的加密算法。何为密钥流呢?假设要加密的数据长N个字节,那么我通过某种算法,也产生一串N字节的数据,然后把这两串N字节数据按位异或(XOR),就得到了密文。把密文与这串密钥流再XOR,就能重新得到明文。而这一串由某种算法产生的N字节,或者说8N位,就叫做密钥流,而该算法就叫做密钥流生成算法。所有基于密钥流的加密算法的区别就在于密钥流的生成方式的不同。只要生成了与数据等长的密钥流,那么加密、解密方式都是把数据与密钥流做异或运算。
RC4本质上就是一种密钥流生成算法。它的特点是算法简单、运算效率高,而且非线性度良好。算法简单的特点使得可以使用硬件来实现RC4,如同在很多旧的无线网卡中就是使用硬件来实现WEP加密的。运算效率高使得用软件实现RC4也很便捷、不会占用过多CPU。而非线性度良好,则是RC4广泛使用的重要原因。所谓非线性度好,就是指通过密码产生密钥流容易,而通过密钥流逆推出密码则很难。
RC4 算法的特点是算法简单,运行速度快,而且密钥长度是可变的,密钥长度范围为 1-256 字节。
算法原理
RC4算法主要包括两个部分:1)使用 key-scheduling algorithm (KSA) 算法根据用户输入的秘钥 key 生成 S 盒;2)使用 Pseudo-random generation algorithm (PRGA) 算法生成秘钥流用于加密数据。

利用Key生成S盒——The key-scheduling algorithm (KSA)
KSA算法初始化长度为 256 的 S 盒。第一个 for 循环将 0 到 255 的互不重复的元素装入 S 盒;第二个 for 循环根据密钥打乱 S 盒。
for i from 0 to 255
S[i] := i
endfor
j := 0
for i from 0 to 255
j := (j + S[i] + key[i mod keylength]) mod 256
swap values of S[i] and S[j]
endfor
利用S盒生成密钥流——The pseudo-random generation algorithm(PRGA)
Pseudo-random generation algorithm (PRGA) 算法根据 S 盒生成与明文长度相同的秘钥流,使用秘钥流加密明文。秘钥流的生成如下图所示:

循环体中每收到一个字节,a 和 b 定位S盒中的一个元素,并与输入字节异或,得到密文 k;同时,c 还改变了 S 盒。由于异或运算的特性,使得加密与解密过程一致。如果输入的是明文,输出的就是密文;如果输入的是密文,输出的就是明文。
i := 0
j := 0
while GeneratingOutput:
i := (i + 1) mod 256 // a
j := (j + S[i]) mod 256 // b
swap values of S[i] and S[j] // c
K := inputByte ^ S[(S[i] + S[j]) mod 256] // d
output K
endwhile
DES
美国国家标准局1973年开始研究除国防部外的其它部门的计算机系统的数据加密标准,于1973年5月15日和1974年8月27日先后两次向公众发出了征求加密算法的公告。加密算法要达到的目的(通常称为DES 密码算法要求)主要为以下四点:
提供高质量的数据保护,防止数据未经授权的泄露和未被察觉的修改;
具有相当高的复杂性,使得破译的开销超过可能获得的利益,同时又要便于理解和掌握;
DES密码体制的安全性应该不依赖于算法的保密,其安全性仅以加密密钥的保密为基础;
实现经济,运行有效,并且适用于多种完全不同的应用。
1977年1月,美国政府颁布:采纳IBM公司设计的方案作为非机密数据的正式数据加密标准(DES Data Encryption Standard)。
DES全称为Data Encryption Standard,即数据加密标准,是一种使用密钥加密的块算法,1977年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),并授权在非密级政府通信中使用,随后该算法在国际上广泛流传开来。它基于使用56位密钥的对称算法。这个算法因为包含一些机密设计元素,相对短的密钥长度以及怀疑内含美国国家安全局(NSA)的后门而在开始时有争议,DES因此受到了强烈的学院派式的审查,并以此推动了现代的块密码及其密码分析的发展。
DES现在已经不是一种安全的加密方法,主要因为它使用的56位密钥过短。1999年1月,distributed.net与电子前哨基金会合作,在22小时15分钟内即公开破解了一个DES密钥。也有一些分析报告提出了该算法的理论上的弱点,虽然在实际中难以应用。为了提供实用所需的安全性,可以使用DES的派生算法3DES来进行加密,虽然3DES也存在理论上的攻击方法。在2001年,DES作为一个标准已经被高级加密标准(AES)所取代。另外,DES已经不再作为国家标准科技协会(前国家标准局)的一个标准。
DES算法简介
DES是一种典型的分组密码—一种将固定长度的明文通过一系列复杂的操作变成同样长度的密文的算法。对DES而言,块长度为64位。同时,DES使用密钥来自定义变换过程,因此算法认为只有持有加密所用的密钥的用户才能解密密文。密钥表面上是64位的,然而只有其中的56位被实际用于算法,其余8位可以被用于奇偶校验,并在算法中被丢弃。因此DES的有效密钥长度仅为56位。
DES设计中使用了分组密码设计的两个原则:混淆(confusion)和扩散(diffusion),其目的是抗击敌手对密码系统的统计分析。混淆是使密文的统计特性与密钥的取值之间的关系尽可能复杂化,以使密钥和明文以及密文之间的依赖性对密码分析者来说是无法利用的。扩散的作用就是将每一位明文的影响尽可能迅速地作用到较多的输出密文位中,以便在大量的密文中消除明文的统计结构,并且使每一位密钥的影响尽可能迅速地扩展到较多的密文位中,以防对密钥进行逐段破译。
DES加密的算法框架如下:

首先要生成一套加密密钥,从用户处取得一个64位长的密码口令,然后通过等分、移位、选取和迭代形成一套16个加密密钥,分别供每一轮运算中使用。
DES对64位(bit)的明文分组M进行操作,M经过一个初始置换IP,置换成m0。将m0明文分成左半部分和右半部分m0 = (L0,R0),各32位长。然后进行16轮完全相同的运算(迭代),这些运算被称为函数f,在每一轮运算过程中数据与相应的密钥结合。
在每一轮中,密钥位移位,然后再从密钥的56位中选出48位。通过一个扩展置换将数据的右半部分扩展成48位,并通过一个异或操作替代成新的48位数据,再将其压缩置换成32位。这四步运算构成了函数f。然后,通过另一个异或运算,函数f的输出与左半部分结合,其结果成为新的右半部分,原来的右半部分成为新的左半部分。将该操作重复16次。
经过16轮迭代后,左,右半部分合在一起经过一个末置换(数据整理),这样就完成了加密过程。
分组加密中的工作模式
分组加密算法是按分组大小来进行加解密操作的,如DES算法的分组是64位,而AES是128位,但实际明文的长度一般要远大于分组大小,这样的情况如何处理呢?这正是"mode of operation"即工作模式要解决的问题:明文数据流怎样按分组大小切分,数据不对齐的情况怎么处理等等。早在1981年,DES算法公布之后,NIST在标准文献FIPS 81中公布了4种工作模式:
电子密码本:Electronic Code Book Mode (ECB)
密码分组链接:Cipher Block Chaining Mode (CBC)
密文反馈:Cipher Feedback Mode (CFB)
输出反馈:Output Feedback Mode (OFB)
2001年又针对AES加入了新的工作模式:
计数器模式:Counter Mode (CTR)
后来又陆续引入其它新的工作模式,在此仅介绍几种常用的:
ECB:电子密码本模式(electronic codebook mode)
ECB模式只是将明文按分组大小切分,然后用同样的密钥正常加密切分好的明文分组。

ECB的理想应用场景是短数据(如加密密钥)的加密。此模式的问题是无法隐藏原明文数据的模式,因为同样的明文分组加密得到的密文也是一样的。举例来说明:

从ECB的工作原理可以看出,如果明文数据在等分后,两块数据相同则会产生相同的加密数据块,这会辅助攻击者快速判断加密算法的工作模式,而将攻击资源聚集在破解某一块数据即可,一旦成功则意味着全文破解,大大提升了攻击效率。为了解决这一缺陷,设计者提出了更多的分组密码工作模式,这些模式下各组数据的加密过程彼此产生关联,尽最大可能混淆数据。
CBC:密码分组链接模式(cipher block chaining Triple)
此模式是1976年由IBM所发明,引入了IV(初始化向量:Initialization Vector)的概念。IV是长度为分组大小的一组随机,通常情况下不用保密,不过在大多数情况下,针对同一密钥不应多次使用同一组IV。 CBC要求第一个分组的明文在加密运算前先与IV进行异或;从第二组开始,所有的明文先与前一分组加密后的密文进行异或。(原理有没有和区块链(blockchain)一致,可以算是区块链的鼻祖)

CBC模式相比ECB实现了更好的模式隐藏,但因为其将密文引入运算,加解密操作无法并行操作。同时引入的IV向量,还需要加、解密双方共同知晓方可。
CFB:密文反馈模式(Cipher FeedBack)
与CBC模式类似,但不同的地方在于,CFB模式先生成密码流字典,然后用密码字典与明文进行异或操作并最终生成密文。后一分组的密码字典的生成需要前一分组的密文参与运算。

CFB模式是用分组算法实现流算法,明文数据不需要按分组大小对齐。
OFB:输出反馈模式(Output Feedbaek)
OFB模式与CFB模式不同的地方是:生成字典的时候会采用明文参与运算,CFB采用的是密文。

CTR:计数器模式(counter mode)
上面的几种工作模式都存在一个共性:数据块彼此之间关联,当前块的解密依赖前面的密文块,因此不能随机访问任意加密块。这样会使得用户为了获取其中一点数据而不得不解密所有数据,当数据量大时效率较低。
CTR模式同样会产生流密码字典,但同是会引入一个计数,以保证任意长时间均不会产生重复输出。

CTR模式只需要实现加密算法以生成字典,明文数据与之异或后得到密文,反之便是解密过程。CTR模式可以采用并行算法处理以提升吞量,另外加密数据块的访问可以是随机的,与前后上下文无关。
CCM:Counter with CBC-MAC
CCM模式,全称是Counter with Cipher Block Chaining-Message Authentication Code,是CTR工作模式和CMAC认证算法的组合体,可以同时数据加密和鉴别服务。
明文数据通过CTR模式加密成密文,然后在密文后面再附加上认证数据,所以最终的密文会比明文要长。具体的加密流程如下描述:先对明文数据认证并产生一个tag,在后续加密过程中使用此tag和IV生成校验值U。然后用CTR模式来加密原输入明文数据,在密文的后面附上校验码U。
GCM:伽罗瓦计数器模式
类型CCM模式,GCM模式是CTR和GHASH的组合,GHASH操作定义为密文结果与密钥以及消息长度在GF(2^128)域上相乘。GCM比CCM的优势是在于更高并行度及更好的性能。TLS 1.2标准使用的就是AES-GCM算法,并且Intel CPU提供了GHASH的硬件加速功能
补充信息
与分组密码相对应的便是序列密码,又称流密码,是指利用密钥通过复杂的密码算法产生大量的伪随机位流,对明文数据流进行加密。在进行解密时,用同样的密钥和算法产生相同的伪随机位流,用以还原明文数据流。目前,公开的序列密码算法主要有RC4、SEAL等。序列密码以一个元素(一个字母或一个比特)作为基本的处理单元,具有转换速度快、低错误传播的优点,硬件实现简单;但加密结果混淆度低、且数据的小幅度变化敏感性低,即插入修改较少的数据,加密结果不会发生大幅变化,这样会给攻击者提供较多分析素材。
总结
ECB是不推荐的方式,Key相同时,相同的明文在不同的时候产生相同的明文,容易遭到字典攻击,CBC由于加入了向量参数,一定程度上抵御了字典工具,但缺点也随之而来,一旦中间一个数据出错或丢失,后面的数据将受到影响,CFB与CBC类似,好处是明文和密文不用是8bit的整数倍,中间一个数据出错,只影响后面的几个块的数据,OFB比CFB方式,一旦一个数据出错,不会影响后面的数据,但安全性降低;因此,推荐使用CFB方式,但每个数据包单独加密,否则一个数据包丢失,需要做很多容错处理;当然,具体问题也要具体分析,对于只需要“特定安全性”,不需要“计算安全性”以上的软件,也可以使用ECB模式,与其它块密码相似,DES自身并不是加密的实用手段,而必须以某种工作模式进行实际操作。
参考链接:
https://github.com/matt-wu/AES
http://www.freebuf.com/articles/database/130521.html
分组加密中的填充算法
在分组加密算法中(例如DES),我们首先要将原文进行分组,然后每个分组进行加密,然后组装密文。其中有一步是分组。如何分组?假设我们现在的数据长度是24字节,BlockSize是8字节,那么很容易分成3组,一组8字节,如果现有的待加密数据不是BlockSize的整数倍,那该如何分组?
例如,有一个17字节的数据,BlockSize是8字节,怎么分组?我们可以对原文进行填充(padding),将其填充到8字节的整数倍。假设使用PKCS#5进行填充(以下都是以PKCS#5为示例),BlockSize是8字节(64bit):
待加密数据原长度为1字节:0x41
填充后:0x410x070x070x070x070x070x070x07
待加密数据原长度为2字节:0x410x41
填充后:0x410x410x060x060x060x060x060x06
待加密数据原长度为3字节:0x410x410x41
填充后:0x410x410x410x050x050x050x050x05
待加密数据原长度为4字节:0x410x410x410x41
填充后:0x410x410x410x410x040x040x040x04
待加密数据原长度为5字节:0x410x410x410x410x41
填充后:0x410x410x410x410x410x030x030x03
待加密数据原长度为6字节:0x410x410x410x410x410x41
填充后:0x410x410x410x410x410x410x020x02
待加密数据原长度为7字节:0x410x410x410x410x410x410x41
填充后:0x410x410x410x410x410x410x410x01
待加密数据原长度为8字节:0x410x410x410x410x410x410x410x41
填充后:0x410x410x410x410x410x410x410x410x080x080x080x080x080x080x080x08
为啥当为整数倍时,还是要多增加8个0x08?假设当x是8的整数倍时,不多填充8个0x08:当解密后时,我看到了解密后的数据的末尾的最后一个字节,这个字节恰好是0x01,那你说,这个字节是填充上去的呢?还是实际的数据呢?
PKCS5Padding与PKCS7Padding的区别
PKCS5Padding与PKCS7Padding基本上是可以通用的。在PKCS5Padding中,明确定义Block的大小是8位,而在PKCS7Padding定义中,对于块的大小是不确定的,可以在1-255之间,填充值的算法都是一样的:
pad = k - (l mod k) //k=块大小,l=数据长度,如果k=8, l=9,则需要填充额外的7个byte的7
可以得出:Pkcs5是Pkcs7的特例(Block的大小始终是8位)。当Block的大小始终是8位的时候,Pkcs5和Pkcs7是一样的。
DES与3DES
3DES(即Triple DES)是DES向AES过渡的加密算法,它使用3条56位的密钥对数据进行三次加密,是DES的一个更安全的变形。它以DES为基本模块,通过组合分组方法设计出分组加密算法。比起最初的DES,3DES更为安全。该方法使用两个密钥,执行三次DES算法,加密的过程是加密-解密-加密,解密的过程是解密-加密-解密。
3DES加密过程为:C=Ek3(Dk2(Ek1(P)))
3DES解密过程为:P=Dk1(EK2(Dk3(C)))
采用两个密钥进行三重加密的好处有:
两个密钥合起来有效密钥长度有112bit,可以满足商业应用的需要,若采用总长为168bit的三个密钥,会产生不必要的开销。
加密时采用加密-解密-加密,而不是加密-加密-加密的形式,这样有效的实现了与现有DES系统的向后兼容问题。因为当K1=K2时,三重DES的效果就和原来的DES一样,有助于逐渐推广三重DES。
三重DES具有足够的安全性,目前还没有关于攻破3DES的报道。
AES
上文的数据加密标准(Data Encryption Standard: DES)的密钥长度是56比特,因此算法的理论安全强度是256。但二十世纪中后期正是计算机飞速发展的阶段,元器件制造工艺的进步使得计算机的处理能力越来越强,DES将不能提供足够的安全性。1997年1月2号,美国国家标准技术研究所(National Institute of Standards and Technology: NIST)宣布希望征集高级加密标准(Advanced Encryption Standard: AES),用以取代DES。AES评判要求:
NIST在征集算法的时候就提出了几项硬性要求:
分组加密算法:支持128位分组大小,128/192/256位密钥
安全性不低于3DES,但实施与执行要比3DES的更高效
优化过的ANSI C的实现代码
KAT(Known-Answer tests)及MCT(Monte Carlo Tests)测试及验证
软件及硬件实现的便捷
可抵御已知攻击
AES得到了全世界很多密码工作者的响应,先后有很多人提交了自己设计的算法。第一轮共有15种算法入选,其中5种算法入围了决赛,分别是:Rijndael,Serpent,Twofish,RC6和MARS。又经过3年的验证、评测及公众讨论之后Rijndael算法最终入选。Rijndael是一个分组密码算法族,由比利时学者Joan Daemen和Vincent Rijmen所提出的,算法的名字就由两位作者的名字组合而成。其分组长度包括128比特、160比特、192比特、224比特、256比特,密钥长度也包括这五种长度,但是最终AES只选取了分组长度为128比特,密钥长度为128比特、192比特和256比特的三个版本。
Rijndael的优势在于集安全性、性能、效率、可实现性及灵活性与一体。Rijndael设计思想:
安全性(Security) 算法足够强,抗攻击
经济性(Efficiency) 算法运算效率高
密钥捷变(Key Agility) 更改密钥所引入的损失尽量小,即最小消耗的密钥扩展算法
适应性 (Versatility) 适用于不同的CPU架构,软件或硬件平台的实现
设计简单(Simplicity) 轮函数的设计精简,只是多轮迭代
AES的算法原理
加密算法的一般设计准则
混淆 (Confusion) 最大限度地复杂化密文、明文与密钥之间的关系,通常用非线性变换算法达到最大化的混淆。
扩散 (Diffusion) 明文或密钥每变动一位将最大化地影响密文中的位数,通常采用线性变换算法达到最大化的扩散。
对Rijndael算法来说解密过程就是加密过程的逆向过程。下图为AES加解密的流程,从图中可以看出:1)解密算法的每一步分别对应加密算法的逆操作,2)加解密所有操作的顺序正好是相反的。正是由于这几点(再加上加密算法与解密算法每步的操作互逆)保证了算法的正确性。

Rijndael算法是基于代换-置换网络(SPN,Substitution-permutation network)的迭代算法。明文数据经过多轮次的转换后方能生成密文,每个轮次的转换操作由轮函数定义。轮函数任务就是根据密钥编排序列(即轮密码)对数据进行不同的代换及置换等操作。

图左侧为轮函数的流程,主要包含4种主要运算操作:字节代换(SubByte)、行移位(ShiftRow)、列混合(MixColumn)、轮密钥加(AddRoundKey)。
图右侧为密钥编排方案,在Rijndael中称为密钥扩展算法(KeyExpansion)。
轮函数
我们已经得知轮函数主要包含4种运算,但不同的运算轮所做的具体运的算组合并不相同。主要区别是初始轮(Round: 0)和最后一轮(Round: Nr),所有中间轮的运算都是相同的,会依次进行4种运算,即:
字节代换(SubByte)
行移位(ShiftRow)
列混合(MixColumn)
轮密钥加(AddRoundKey)
Rijndael算法支持大于128位的明文分组,所以需要列数更多的矩阵来描述。Rijndael轮函数的运算是在特殊定义的有限域GF(256)上进行的。有限域(Finite Field)又名伽罗瓦域(Galois field),简单言之就是一个满足特定规则的集合,集合中的元素可以进行加减乘除运算,且运算结果也是属于此集合。根据Rinjdael算法的定义,加密轮数会针对不同的分组及不同的密钥长度选择不同的数值:

AES标准只支持128位分组(Nb = 4)的情况。AES标准算法将128位的明文,以特定次序生成一个4×4的矩阵(每个元素是一个字节,8位),即初始状态(state),经由轮函数的迭代转换之后又将作为下一轮迭代的输入继续参与运算直到迭代结束。
轮函数拆解:字节代换(Substitute Bytes)
字节代换(SubBytes)是对state矩阵中的每一个独立元素于置换盒(Substitution-box,S盒)中进行查找并以此替换输入状态的操作。字节代换是可逆的非线性变换,也是AES运算组中唯一的非线性变换。字节代换逆操作也是通过逆向置换盒的查找及替换来完成的,主要功能是通过S盒完成一个字节到另外一个字节的映射。

S盒是由一个有限域GF(256)上的乘法求逆并串联线性仿射变换所构造出来的,不是一个随意构造的简单查询表。S因其运算复杂,众多的AES 软件及硬件实现直接使用了查找表(LUP, Look-up table),但查询表的方式并不适合所有场景,针对特定的硬件最小化面积设计需求,则要采用优化的组合逻辑以得到同价的S盒替换。盒是事先设计好的16×16的查询表,即256个元素。S盒用于提供密码算法的混淆性。S盒的详细构造方法可以参考文献。这里直接给出构造好的结果,下图(a)为S盒,图(b)为S-1(S盒的逆)。S和S-1分别为16×16的矩阵,完成一个8比特输入到8比特输出的映射,输入的高4-bit对应的值作为行标,低4-bit对应的值作为列标。

轮函数拆解:行移位(Shift Rows)
行移位主要目的是实现字节在每一行的扩散,属于线性变换。行移位是一个4×4的矩阵内部字节之间的置换,用于提供算法的扩散性。
1) 正向行移位
正向行移位用于加密,其原理图如下。其中:第一行保持不变,第二行循环左移8比特,第三行循环左移16比特,第四行循环左移24比特。假设矩阵的名字为state,用公式表示如下:state[i][j] = state[i][(j+i)%4];其中i、j属于[0,3]。

2) 逆向行移位
逆向行移位即是相反的操作,即:第一行保持不变,第二行循环右移8比特,第三行循环右移16比特,第四行循环右移24比特。用公式表示如下:state’[i][j] = state[i][(4+j-i)%4];其中i、j属于[0,3]。
轮函数拆解:列混合(Mix Columns)
列混合是通过将state矩阵与常矩阵C相乘以达成在列上的扩散,属于代替变换。列混合是Rijndael算法中最复杂的一步,其实质是在有限域GF(256)上的多项式乘法运算。

1) 正向列混淆
正向列混淆的原理图如下:

根据矩阵的乘法可知,在列混淆的过程中,每个字节对应的值只与该列的4个值有关系。此处的乘法和加法都是定义在GF(28)上的,需要注意如下几点:
将某个字节所对应的值乘以2,其结果就是将该值的二进制位左移一位,如果原始值的最高位为1,则还需要将移位后的结果异或00011011;
乘法对加法满足分配率,例如:07·S0,0=(01⊕02⊕04)·S0,0= S0,0⊕(02·S0,0)(04·S0,0)
此处的矩阵乘法与一般意义上矩阵的乘法有所不同,各个值在相加时使用的是模28加法(异或运算)。
下面举一个例子,假设某一列的值如下图,运算过程如下:


在计算02与C9的乘积时,由于C9对应最左边的比特为1,因此需要将C9左移一位后的值与(0001 1011)求异或。同理可以求出另外几个值。
2) 逆向列混淆
逆向列混淆的原理图如下:

由于:

说明两个矩阵互逆,经过一次逆向列混淆后即可恢复原文。
轮函数拆解:轮密钥加(Add Round Key)
密钥加是将轮密钥简单地与状态进行逐比特异或。这个操作相对简单,其依据的原理是“任何数和自身的异或结果为0”。加密过程中,每轮的输入与轮子密钥异或一次;因此,解密时再异或上该轮的轮子密钥即可恢复。

密钥扩展算法(Key Expansion)
AES加解密中每轮的密钥分别由种子密钥经过密钥扩展算法得到。算法中16字节的明文、密文和轮子密钥都以一个4×4的矩阵表示。
密钥扩展算法是Rijndael的密钥编排实现算法,其目的是根据种子密钥(用户密钥)生成多组轮密钥。轮密钥为多组128位密钥,对应不同密钥长度,分别是11,13,15组。

密钥扩展的原理图如下:

密钥扩展过程说明:
1) 将种子密钥按图(a)的格式排列,其中k0、k1、……、k15依次表示种子密钥的一个字节;排列后用4个32比特的字表示,分别记为w[0]、w[1]、w[2]、w[3];
2) 按照如下方式,依次求解w[j],其中j是整数并且属于[4,43];
3) 若j%4=0,则w[j]=w[j-4]⊕g(w[j-1]),否则w[j]=w[j-4]⊕w[j-1];
函数g的流程说明:
a) 将w循环左移8比特;
b) 分别对每个字节做S盒置换;
c) 与32比特的常量(RC[j/4],0,0,0)进行异或,RC是一个一维数组,其值如下。(RC的值只需要有10个,而此处用了11个,实际上RC[0]在运算中没有用到,增加RC[0]是为了便于程序中用数组表示。由于j的最小取值是4,j/4的最小取值则是1,因此不会产生错误。)
RC = {0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36}
动画演示加密过程:
Enrique Zabala创建了一个AES-128加密算法的动画演示,清楚、直观地介绍了轮函数执行的过程。
波士顿大学的Howard Straubing做了这么一个动画来展示AES加密算法的演示。
参考链接:
https://github.com/matt-wu/AES/
其他参考资料:

AES算法的使用
在正式软件运用中并不推荐自己编写代码,很多开源项目如Linux,OPENSSL,SRTP等都有非常高效的实现。由于是分组加密,所以在使用的时候设定分组加密工作模式和填充算法。
Blowfish
Blowfish是一个对称密钥加密分组密码算法,由布鲁斯·施奈尔于1993年设计,现已应用在多种加密产品。Blowfish算法由于分组长度太小已被认为不安全,施奈尔更建议在现代应用中使用Twofish密码。
施奈尔设计的Blowfish算法用途广泛,意在替代老旧的DES及避免其他算法的问题与限制。Blowfish刚刚研发出的时候,大部分其他加密算法是专利所有的或属于商业(政府)机密,所以发展起来非常受限制。施奈尔则声明Blowfish的使用没有任何限制,任何国家任何人任何时候都可以随意使用Blowfish算法。
Blowfish主要包括关键的几个S盒和一个复杂的核心变换函数。
Bcrypt
bcrypt是一个由Niels Provos以及David Mazières根据Blowfish加密算法所设计的密码散列函数,于1999年在USENIX中展示。实现中bcrypt会使用一个加盐的流程以防御彩虹表攻击,同时bcrypt还是适应性函数,它可以借由增加迭代之次数来抵御日益增进的电脑运算能力透过暴力法破解。
由bcrypt加密的文件可在所有支持的操作系统和处理器上进行转移。它的口令必须是8至56个字符,并将在内部被转化为448位的密钥。然而,所提供的所有字符都具有十分重要的意义。密码越强大数据就越安全。
除了对数据进行加密,默认情况下,bcrypt在删除数据之前将使用随机数据三次覆盖原始输入文件,以阻挠可能会获得您的计算机数据的人恢复数据的尝试。如果不想使用此功能,可设置禁用此功能。
具体来说,bcrypt使用保罗·柯切尔的算法实现,随bcrypt一起发布的源代码对原始版本作了略微改动。
使用参考案例
Dropbox账户密码存储实践
众所周知,存储明文密码是一件很糟糕的事情。如果数据库存储了明文密码,一旦数据泄漏,那么用户账号就危险了。因为这个原因,早在1976年,工业界就提出了一套使用单向哈希机制来安全地存储密码的标准(从Unix Crypt开始)。很不幸的是,尽管这种方式可以阻止你直接读取到密码,但是所有的哈希机制都不能阻止攻击者在离线环境下暴力破解它,攻击者只需要遍历一个可能包含正确密码的列表,对每个可能的密码进行哈希然后跟获取到的密码(使用哈希机制存储的密码)比对即可。在这种环境下,安全哈希函数如SHA在用于密码哈希的时候有一个致命的缺陷,那就是它们运算起来太快了。一个现代的商用CPU一秒钟可以生成数百万个SHA256哈希值。一些特殊的GPU集群的计算速度甚至可以达到每秒数十亿次。
过去的这些年,为了应对攻击,Dropbox对密码哈希方法进行了数次升级。他们的密码存储方案依赖三个不同层级的密码保护,如下图所示:

Dropbox采用 Bcrypt 作为核心哈希算法,每个用户都有一个独立的salt以及一个加密的key(这个key也可以是一个全局的,通常也叫pepper),salt和key是分开存储的。与基础的 Bcrypt 算法在一些重要的方面是不同的:
首先,用户的明文密码通过 SHA512 算法转换成了一个哈希值。这一步主要是针对Bcrypt的两个突出的问题。有些Bcrypt的实现中会将用户输入截取为72个字节大小以降低密码熵,而另外有一些实现并没有截取用户输入导致其容易受到DoS攻击,因为它们允许任意长度的密码输入。通过使用SHA,可以快速的将一些的确很长的密码转换为一个512比特的固定长度,解决了上述两个问题,即避免降低密码熵和预防DoS攻击。
然后,对SHA512哈希后的值使用bcrypt算法再次哈希,使用的工作因子是10,每个用户都有一个单独的salt。不像其他的哈希算法比如SHA等,Bcrypt算法很慢,它很难通过硬件和GPU加速。设置工作因子为10,在服务器上执行一次bcrypt大概需要100毫秒。
最后,使用Bcrypt哈希过后的结果再次使用AES256算法进行加密,使用的密钥是所有用户统一的,称之为pepper。pepper是基于深度考量的一种防御措施,pepper以一种攻击者难以发现的方式存储起来(比如不要放在数据库的表中)。由此,如果只是密码被拖库了,通过AES256加密过的哈希密码对于攻击者来说毫无用处。
为什么不使用scrypt或argon2?
Dropbox曾考虑过使用Scrypt,但是我们对Dropbox有更多的经验。关于这几种算法哪种更好的讨论一直都有,大部分的安全领域的专家都认为scrypt和bcrypt的安全性上相差无几。
Dropbox考虑在下一次升级中使用argon2算法:因为在采用当前的方案的时候,argon2还没有赢得 Password Hashing Competition。此外,从1999年以来,Bcrypt还没有发现有任何重大的攻击存在。
为什么使用一个全局的密钥(pepper)替代哈希函数
如前面提到的,采用一个全局的密钥是我们深度权衡后的一个防御措施,而且,pepper是单独存储的。但是,单独存储pepper也意味着要考虑pepper泄露的可能性。如果只是用pepper对密码进行哈希,那么一旦pepper泄露,无法从哈希后的结果反解得到之前bcrypt哈希过的密码值。作为一个替代方案,Dropbox使用了AES256加密算法。AES256算法提供了差不多的安全性,同时还可以反解回原来的值。尽管AES256这个加密函数的输入是随机的,Dropbox还是额外加上了一个随机的初始化向量(IV)来增强安全性。下一步,Dropbox考虑将pepper存储到一个硬件安全模块(HSM),这虽然是一个相当复杂的任务,但是它能极大的降低pepper泄露的风险。同时,也计划在下一次升级中增强Bcrypt的强度。
展望
Dropbox相信使用SHA512,加上bcrypt和AES256是当前保护密码最稳妥和流行的方法之一。同时所谓道高一尺魔高一丈。密码哈希程序只是加固Dropbox的众多举措之一,Dropbox还部署了额外的保护措施-比如针对暴力攻击者密码尝试次数的速度限制,验证码,以及其他一些方法等。
原文链接:How Dropbox securely stores your passwords
用户密码加密存储问答
我们数据库的权限管理十分严格,敏感信息开发工程师都看不到,密码明文存储不行吗?
不行。存储在数据库的数据面临很多威胁,有应用程序层面、数据库层面的、操作系统层面的、机房层面的、员工层面的,想做到百分百不被黑客窃取,非常困难。如果密码是加密之后再存储,那么即便被拖库,黑客也难以获取用户的明文密码。可以说,密码加密存储是用户账户系统的底线,它的重要性,相当于独自出远门时缝在内衣里钱,虽然用到他们的概率不大,但关键时刻能救命。
那用加密算法比如AES,把密码加密下再存,需要明文的时候我再解密。
不行。这涉及到怎么保存用来加密解密的密钥,虽然密钥一般跟用户信息分开存储,且业界也有一些成熟的、基于软件或硬件的密钥存储方案。但跟用户信息的保存一样,想要密钥百分百不泄露,不可能做到。用这种方式加密密码,能够降低黑客获取明文密码的概率。但密钥一旦泄露,用户的明文密码也就泄露了,不是一个好方法。另外用户账户系统不应该保存用户的明文密码,在用户忘记密码的时候,提供重置密码的功能而不是找回密码。
保存所有密码的HASH值,比如MD5。是不是就可以了?
不是所有的HASH算法都可以,准确讲应该是Cryptographic Hash。Cryptographic Hash具有如下几个特点:
给定任意大小任意类型的输入,计算hash非常快;
给定一个hash,没有办法计算得出该hash所对应的输入;
对输入做很小改动,hash就会发生很大变化;
没有办法计算得到两个hash相同的输入;
虽然不是为加密密码而设计,但其第2、3、4三个特性使得Cryptographic Hash非常适合用来加密用户密码。常见的Cryptographic Hash有MD5、SHA-1、SHA-2、SHA-3/Keccak、BLAKE2。从1976年开始,业界开始使用Cryptographic Hash加密用户密码,最早见于Unix Crypt。但MD5、SHA-1已被破解,不适合再用来保存密码。
那我保存用户密码的SHA256值。
不行。黑客可以用查询表或彩虹表来破解用户密码。注意是破解密码不是破解sha256,能根据sha256破解密码的原因是,用户密码往往需要大脑记忆、手工输入,所以不会太复杂,往往具有有限的长度、确定的取值空间。
短的取值简单的密码可以用查询表破解
比如8位数字密码,一共只有10^8=100000000种可能。一亿条数据并不算多,黑客可以提前吧0-99999999的sha256都计算好,并以sha256做key密码为value存储为一个查询表,当给定sha256需要破解时,从表中查询即可。
取值相对复杂,且长度较长的密码,可以用彩虹表破解
比如10位,允许数字、字母大小写的密码,一共有(10+26+26)^10~=84亿亿种可能,记录非常之多难以用查询表全部保存起来。这时候黑客会用一种叫做彩虹表的技术来破解,彩虹表用了典型的计算机世界里解决问题的思路,时间空间妥协。在这个例子里面,空间不够,那就多花一些时间。在彩虹表中,可以将全部的sha256值转化为长度相同的若干条hash链,只保存hash链的头和尾,在破解的时候先查询得到sha256存在于哪条hash链中,然后计算这一条hash链上的所有sha256,通过实时比对来破解用户密码。

上图图展示了一个hash链长度为3的彩虹表,因为在hash链中需要将hash值使用R函数映射回密码取值空间,为了降低R函数的冲突概率,长度为K的hash链中,彩虹表会使用k个R函数,因为每次迭代映射回密码空间使用的R函数不一样,这种破解方法被称作彩虹表攻击。
实际的情况Hash链要比远比上例更长,比如我们的例子中全部的84亿亿个sha256存不下,可以转化为840亿条长度为1千万的sha链。对彩虹表原理感兴趣的话,可以阅读它的维基百科。
网路上甚至有一些已经计算好的彩虹表可以直接使用,所以直接保存用户密码的sha256是非常不安全的。
怎样避免彩虹表攻击?
简单讲,就是加盐。一般来讲用户密码是个字符串key、盐是我们生成的字符串salt。原来我们保存的是key的hash值HASH(key),现在我们保存key和salt拼接在一起的hash值HASH(key+salt)。这样黑客提前计算生成的彩虹表,就全都失效了。
盐应该怎么生成,随机生成一个字符串?
这是个好问题,并不是加个盐就安全了,盐的生成有很多讲究。
使用CSPRNG(Cryptographically Secure Pseudo-Random Number Generator)生成盐,而不是普通的随机数算法;CSPRNG跟普通的随机数生成算法,比如C语言标准库里面的rand()方法,有很大不同。正如它的名字所揭示,CSPRNG是加密安全的,这意味着用它产生的随机数更加随机,且不可预测。常见编程语言都提供了CSPRNG,如下表:
编程语言:CSPRNG
C/C++:CryptGenRandom
Java:Java.security.SecureRandom
PHP:mcrypt_create_iv
Erlang:Crypt:strong_rand_bytes
Linux/Unix上的任何编程语言:读取/dev/random
盐不能太短
想想查询表和彩虹表的原理,如果盐很短,那意味着密码+盐组成的字符串的长度和取值空间都有限。黑客完全可以为密码+盐的所有组合建立彩虹表。
盐不能重复使用
如果所有用户的密码都使用同一个盐进行加密。那么不管盐有多复杂、多大的长度,黑客都可以很容易的使用这个固定盐重新建立彩虹表,破解你的所有用户的密码。如果你说,我可以把固定盐存起来,不让别人知道啊,那么你应该重新读一下我关于为什么使用AES加密不够安全的回答。即便你为每一个用户生成一个随机盐,安全性仍然不够,因为这个盐在用户修改密码时重复使用了。应当在每一次需要保存新的密码时,都生成一个新的盐,并跟加密后的hash值保存在一起。
注意:有些系统用一个每个用户都不同的字段,uid、手机号、或者别的什么,来作为盐加密密码。这不是一个好主意,这几乎违背了上面全部三条盐的生成规则。
那我自己设计一个黑客不知道的HASH算法,这样你的那些破解方法就都失效了。
不可以。首先如果你不是一个密码学专家,你很难设计出一个安全的hash算法。不服气的话,你可以再看一遍上面我关于Cryptographic Hash的描述,然后想一想自己怎么设计一个算法可以满足它的全部四种特性。就算你是基于已有的Cryptographic Hash的基础上去设计,设计完之后,也难以保证新算法仍然满足Cryptographic Hash的要求。而一旦你的算法不满足安全要求,那么你给了黑客更多更容易破解用户密码的方法。
即便你能设计出一个别人不知道的Cryptographic Hash算法,你也不能保证黑客永远都不知道你的算法。黑客往往都有能力访问你的代码,想想柯克霍夫原则或者香农公里:
密码系统应该就算被所有人知道系统的运作步骤,仍然是安全的。
为每一个密码都加上不同的高质量的盐,做HASH,然后保存。这样可以了吧?
以前是可以的,现在不行了。计算机硬件飞速发展,一个现代通用CPU能以每月数百万次的速度计算sha256,而GPU集群计算sha256,更是可以达到每秒10亿次以上。这使得暴力破解密码成为可能,黑客不再依赖查询表或彩虹表,而是使用定制过的硬件和专用算法,直接计算每一种可能,实时破解用户密码。
那怎么办呢?回想上面关于Cryptographic Hash特性的描述,其中第一条:
给定任意大小任意类型的输入,计算hash非常快
Cryptographic Hash并不是为了加密密码而设计的,它计算非常快的这个特性,在其他应用场景中非常有用,而在现在的计算机硬件条件下,用来加密密码就显得不合适了。针对这一点,密码学家们设计了PBKDF2、BCRYPT、SCRYPT等用来加密密码的Hash算法,称作Password Hash。在他们的算法内部,通常都需要计算Cryptographic Hash很多次,从而减慢Hash的计算速度,增大黑客暴力破解的成本。可以说Password Hash有一条设计原则,就是计算过程能够按要求变慢,并且不容易被硬件加速。
应该使用哪一种Password Hash?
PBKDF2、BCRYPT、SCRYPT曾经是最常用的三种密码Hash算法,至于哪种算法最好,多年以来密码学家们并无定论。但可以确定的是,这三种算法都不完美,各有缺点。其中PBKDF2因为计算过程需要内存少所以可被GPU/ASIC加速,BCRYPT不支持内存占用调整且容易被FPGA加速,而SCRYPT不支持单独调整内存或计算时间占用且可能被ASIC加速并有被旁路攻击的可能。
2013年NIST(美国国家标准与技术研究院)邀请了一些密码学家一起,举办了密码hash算法大赛(Password Hashing Competition),意在寻找一种标准的用来加密密码的hash算法,并借此在业界宣传加密存储用户密码的重要性。大赛列出了参赛算法可能面临的攻击手段:
加密算法破解(原值还原、哈希碰撞等,即应满足Cryptographic Hash的第2、3、4条特性);
查询表/彩虹表攻击;
CPU优化攻击;
GPU、FPGA、ASIC等专用硬件攻击;
旁路攻击。
最终在2015年7月,Argon2算法赢得了这项竞赛,被NIST认定为最好的密码hash算法。不过因为算法过新,目前还没听说哪家大公司在用Argon2做密码加密。
